Stably causal時空
causal時空の計量を少し摂動したものもcausal時空になるとは限らない。
もしなるならその時空のcausalという性質は安定であることになる。
これがstably causal時空である。
まず計量を摂動するということの意味を明確に定義する。
以下に見るように摂動というよりは光円錐を少し“開く”ことに対応する。
時空 $(M,g)$ 上の時間的に向き付けられた計量全体を $Lor(M)$ と書く。
$Lor(M)$ に半順序 $<$ を次のように定める。
$g,g'\in Lor(M)$ に対して、$g$ に関するcausalベクトルが全て $g'$ に関してtimelikeになるとき、$g< g'$ と定める。
時空 $(M,g)$ がstably causal時空 (安定的因果時空) であるとは、計量 $g'$ で $g< g'$ となり、かつ $(M,g')$ がcausal時空となるものが存在するときを言う。
$g_1< g_2$ であるとき、$g_\lambda:=\lambda (1-\lambda)g_1+\lambda g_2>g_1,\ (0\le\lambda\le1)$ であることが簡単に分かる。
stably chronologicalも同様に定義される。
次の命題から分かるようにstably causalとstably chronologicalを区別する必要はない。
stably causalとstably chronologicalは同値である。
stably causalならば明らかにstably chronologicalである。
逆を示すには、stably causalでないならばstably chronologicalでないことを示せばよい。
$(M,g)$ がstably causalでないならば、任意の $g_1>g$ となる計量 $g_1$ に対して、
$g_1>g_2>g$ となる計量 $g_2$ を取ると $g_2$ に関して閉causal曲線 $\gamma$ が存在する。
定義より $\gamma$ は $g_1$ に関して閉chronological曲線である。
よって $(M,g_1)$ はchronologicalでない。
2次元時空はいくらかの側面で特別であり以下はその特別性の一つを示している。
単連結な2次元時空はstably causalである。
任意の単連結な2次元時空はstrongly causalであり、従ってcausalであることから分かる。
stably causal時空の特徴づけとして次の定理がある。
これはstably causalの定義からは全く明らかでなく特筆すべき性質である。
時空 $(M,g)$ に対して以下は同値である。
stably causalである。
time functionが存在する。
temporal functionが存在する。
この定理の証明は長いので概略のみ示す。
詳しくはCiteRef::Sánchez, Miguel.,CiteRef::Bernal.A.N. and Sánchez.M.を参照されたい。
(3)$\Rightarrow$(1)
temporal functionを $T:M\rightarrow\mathbb{R}$ とする。
stably causalという性質は因果的な構造なので共形不変である。
従って適当に共形変換して、$g(\nabla T,\nabla T)=-1$ として、$g=-dT^2+h$ としてよい。
$h$ は $T=const.$ で定義される滑らかな空間的部分多様体に誘導されたリーマン計量である。
このとき、$g_\lambda:=-\lambda dT^2+h,\ \lambda>0$ という計量の族を考えると、$(M,g_\lambda)$ においても $T$ はtemporal functionであるからcausal時空である。
$1<\lambda$ に対して、$g< g_\lambda$ であるからstably causalである。
(1)$\Rightarrow$(2)
$g<\tilde{g}$ でcausalとなる $\tilde{g}$ を一つ取る。
計量の族 $g_\lambda:=g+\frac{\lambda}{2}(\tilde{g}-g),\ 0\le\lambda\le2$ を考えると、$g_\lambda$ は全てcausalである。
$t^-_\lambda$ を $g_\lambda$ に関する過去体積関数とする。
$t^-_\lambda$ を積分して
$$
t(p):=\int^1_0t^-_\lambda(p)d\lambda
$$
を定義すると、これが $(M,g)$ に関してtime functionとなっていることを確かめることができる。
(2)$\Rightarrow$(3)
またstably causal時空の全体はstrongly causal時空の全体の部分集合であることが次の命題から分かる。
stably causal時空はstrongly causal時空である。
time functionを $t$ とする。
任意の点 $p\in M$ と任意の近傍 $U(\ni p)$ が与えられたとき、$p$ の凸近傍 $C_1\subset U$ を取る。
さらに $p$ の凸近傍 $C_2$ で $C_2\subset C_1$ かつ $C_1$ に対して相対コンパクトとなるものを取る。
$t(p)=0$ としてよい。
$q\in C_2$ に対して $\epsilon^+(q):=\min\{t(r);\ r\in J^+(p,C_1)\cap \partial C_2\},\ \epsilon^-(q):=\min\{|t(r)|;\ r\in J^-(p,C_1)\cap \partial C_2\}$ とし、$\epsilon(q):=\min\{\epsilon^+(q),\epsilon^-(q)\}$ と定義する。
$C_1$ 内では $J^\pm$ は連続であり、$\partial C_2$ はコンパクトであるから、$\epsilon(q)$ は連続である。
$p\in W\subset C_2$ となり $C_2$ に対して相対コンパクトとなる近傍 $W$ を取り、$\epsilon_W:=\min\{\epsilon(r);\ r\in W\}$ とする。
$V:=W\cap t^{-1}((-\epsilon_W/2,\epsilon_W/2))$ と置く。
今、$V$ の点を始点とするcausal曲線 $\gamma$ で $U$ を出ていくものは $C_1$ を出ていくからある点 $p'$ において $t(\gamma(p'))>\epsilon_W$ または $t(\gamma(p'))<-\epsilon_W$ となり、$t$ はtime functionであるから $\gamma$ が $V$ に戻ってくることは不可能である。
よって近傍 $V$ は $U$ に対してstrongly causal時空の定義(2)を満たす。
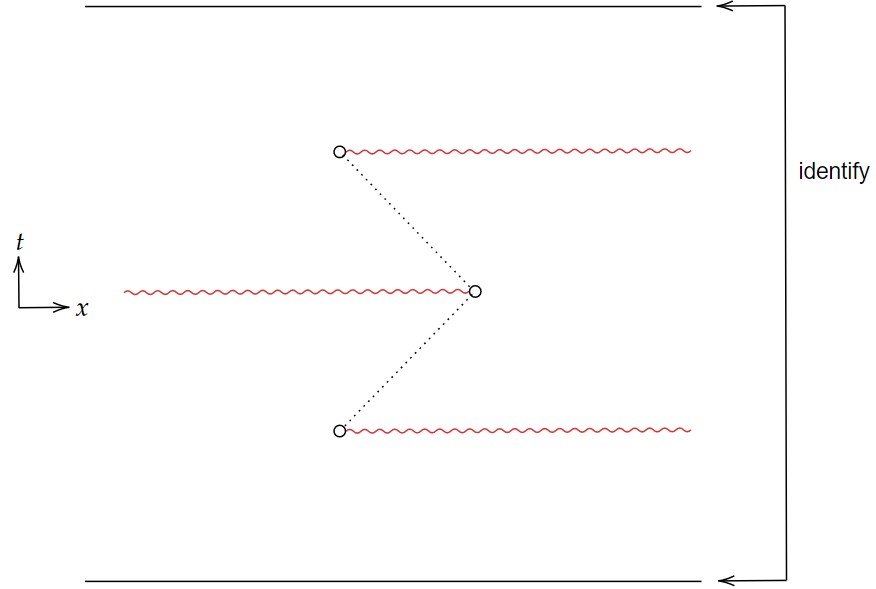
次の例はstrongly causalであるがstably causalではない時空である。
このことからstably causal時空の全体がstrongly causal時空の全体の真部分集合である。
 画像の名前
画像の名前
