Causally Continuous時空
$$$$
stably causal時空にはtime functionが存在した(さらにtemporal functionの存在も同値であった)。
しかしstably causal時空でも体積関数 $t^-$ がtime functionとなるとは限らない。
一般に $t^-$ は連続ではないからである。
$t^-$ が連続となるときは時空の因果構造、特に因果錐が連続であると理解することができるだろう。
distinguishing時空では $t^-$ が一般化time functionであったことを思い出すと次のように定義する。
causally continuous時空
時空 $(M,g)$ がcausally continuous時空であるとは、以下の同値な条件を満たすことである。
$(M,g)$ はdistinguishingであり、かつ $t^\pm$ が連続である。
$t^\pm$ はtime functionである。
これらが同値なことはdistinguishing時空の特徴づけから明らかである。
またstably causal時空の特徴づけから次も明らかである。
causally continuous時空はstably causal時空である。
stably causalだがcausally continuous時空でない時空の例
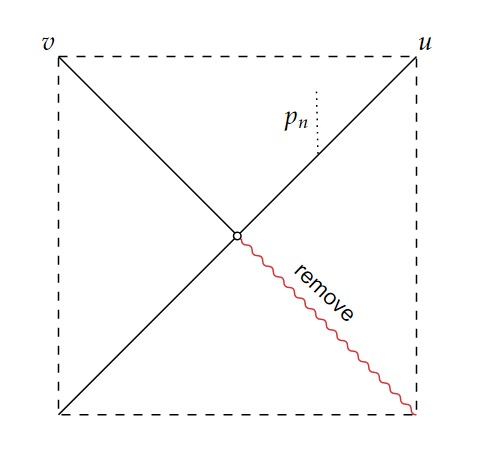
下図のようなMinkowski時空の開部分多様体を考える。
原点及び赤色の波線部分は取り除かれているとする。
このとき、例えば点列 $\{p_n\}$ を考えれば分かるように、明らかに $t^-$ は連続でない。
前ページへ

次ページへ