time separation(時間間隔)
時空の $p< q$ となる2点が時間的にどれぐらい隔たっているかを測ることが出来る。
これが次のtime separation(時間間隔)である。
時空 $(M,g)$ に対して、time separation(時間間隔)$\tau:M\times M\rightarrow\mathbb{R}$ を
$$
\tau(p,q):=\sup\{L(\gamma);\ \gamma:[0,1]\rightarrow Mは\gamma(0)=p,\gamma(1)=qとなる未来向きcausal曲線\}
$$
と定義する。
ただし、$p,q$ を結ぶ未来向きのcausal曲線が存在しないときは、$\tau(p,q)=0$ と定める。
time separationの基本的な性質は次である。
$\tau(p,q)>0\ \Leftrightarrow\ p<< q$
$p\le q\le r$ のとき、$\tau(p,r)\geq\tau(p,q)+\tau(q,r)$ (逆三角不等式)
$\tau(p,q)>0$ とすると、$p,q$ を結ぶ未来向きのcausal曲線 $\alpha$ で $L(\alpha)>0$ となるものが存在する。
$\alpha$ はヌル測地線ではないから端点を固定した変分によりtimelike曲線に変形できる。
従って、$p<< q$ である。
逆は明らかである。$p,q$ を結ぶcausal曲線 $\alpha$ と $q,r$ を結ぶcausal曲線を $\beta$ を適切に選べば、任意の小さい $\delta$ に対して $L(\alpha)\geq\tau(p,q)-\delta/2,\ L(\beta)\geq\tau(q,r)-\delta/2$ となるようにできる。
よって $\tau(p,r)\geq L(\alpha\cup\beta)\geq\tau(p,q)+\tau(q,r)-\delta$ となり、不等式が従う。
一般にtime separationは連続関数ではない。
 画像の名前
画像の名前
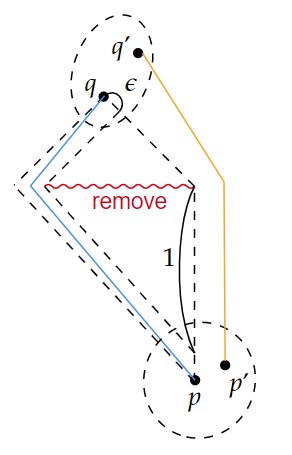
この例では $p,q$ を結ぶtimelike曲線(青線)の長さは、$\epsilon$ を小さく取れば、いくらでも0に近くなるから $\tau(p,q)$ はいくらでも小さくできる。
しかし $p,q$ それぞれの任意の近傍から適当に $p',q'$ を取ると $p',q'$ を結ぶtimelike曲線(黄線)の長さが1に近いものがある。
従って $p,q$ の近くに制限しても $\tau$ が大きくなる範囲が一定値より小さくなるようにすることはできない。
この例から $\tau$ は上半連続ではないことが分かる。
下半連続(上半連続)とは任意に少しだけ小さくなる(大きくなる)近傍があるということであり、詳しくは以下で定義される。
$X$ を位相空間とするとき、写像 $f:X\rightarrow\mathbb{R}$ が点 $p\in X$ において連続であるとは、任意の $\varepsilon>0$ に対して、ある $p$ の近傍 $U$ があって、任意の点列 $\{p_n\}\in U,\ p_n\rightarrow p$ が $-\varepsilon< f(p_n)-f(p)<\varepsilon$ を満たすことである。
$f$ が下半連続であるとは最後の式が $-\varepsilon< f(p_n)-f(p)$ となることであり、同様に上半連続であるとは $f(p_n)-f(p)<\varepsilon$ となることである。
任意の時空においてtime separationは下半連続である。
$\tau(p,q)=0$ のときは定義より $(p,q)$ において下半連続である。
$0<\tau(p,q)<\infty$ とする。
$p,q$ を結ぶtimelike曲線 $\alpha$ で $L(\alpha)>\tau(p,q)-\delta$ となるものが存在する($\delta$ は任意の小さい正数)。
$\alpha$ 上の $p,q$ に十分近い点をそれぞれ $p_0,q_0,\ (p<< p_0,q_0<< q)$ とする(適当な凸近傍内に選べばよい)。
$p,p_0$ を結ぶ測地線を $\overline{pp_0}$、$q_0,q$ を結ぶ測地線を $\overline{q_0q}$ とする。
$p$ の近傍 $V_p$ で任意の $p_1\in V_p$ に対して、$L(\overline{p_1p_0})\geq L(\overline{pp_0})-\delta$ が成り立つものが取れる(凸近傍内ではtimelike曲線の長さは端点に関して連続であり、$p_1=p$ に対してこの不等式は成り立つから)。
同様に、$q$ の近傍 $V_q$ で任意の $q_1\in V_q$ に対して、$L(\overline{q_0q_1})\geq L(\overline{q_0q})-\delta$ が成り立つものが取れる。
よって任意の $p_1\in V_p,\ q_1\in V_q$ に対して、
$$
\begin{aligned}
\tau(p_1,q_1)&\geq L(\overline{p_1p_0})+L(\alpha(p_0\rightarrow q_0))+L(\overline{q_0q_1})
\geq L(\overline{pp_0})+L(\alpha(p_0\rightarrow q_0))+L(\overline{q_0q})-2\delta\\
&\geq L(\alpha(p\rightarrow p_0)+L(\alpha(p_0\rightarrow q_0))+L(\alpha(q_0\rightarrow q))-2\delta\\
&\geq L(\alpha)-2\delta
\geq \tau(p,q)-3\delta
\end{aligned}
$$
となり、下半連続であることが分かる。
