Causally Simple時空
時空 $(M,g)$ が causally simple (因果的単純) 時空であるとは、(i) causalでかつ (ii) 任意の $p\in M$ に対して、$J^\pm(p)$ が閉集合となることである。
上の定義で(i)の条件をdistinguishingにした定義もある。
しかし以下の命題から分かるように上に定義された時空はdistinguishingである。
従って2つの定義は同値である。
(上の定義の意味で)causally simple時空はdistinguishingである。
distinguishingでないと仮定して矛盾を導く。
$p\ne q$ で $I^+(p)=I^+(q)$ となる $p,q$ があるから、点列 $\{q_n\},\ q_n\rightarrow q,\ q<< q_n$ を考えると、$q\in \overline{I^+(q)}=\overline{I^+(p)}=\overline{J^+(p)}=J^+(p)$ となる(左から1つ目の等号はdistinguishingでない時空で常に成り立ち、2つ目の等号は任意の時空で成り立ち、3つ目の等号は(ii)の仮定より成り立つ)。
よって $p< q$ である。
同様に $q< p$ である。
従ってcausal時空でなくなり矛盾する。
この命題の証明からdistinguishingでなく、$J^+$ が閉である時空はcausal時空でないことも分かる。
次の命題はcausally simple時空がcausally continuous時空の部分集合であることを示している。
causally simple時空はcausally continuous時空である。
reflectivityを示す。
$q\in \overline{I^\pm(p)}=J^\pm(p)$ とすると、$p\in J^\mp(q)=\overline{I^\mp(q)}$ である。
(途中)
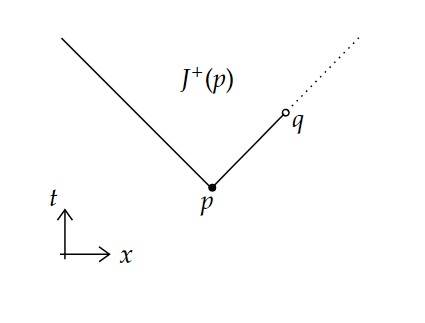
2次元Minkowski時空から一点を取り除いた時空はcausally continuousであるが、causally simpleでない。
実際、下図において $J^+(p)$ は閉集合でない。
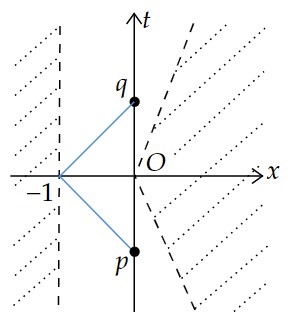
causaly simple時空の因果構造はこれまでの時空に比べればかなり“整っている”が以下の歓迎されない性質を持つことがある。
- ある $p,q$ に対して、$\tau(p,q)=\infty$ となることがある。
- $\tau(p,q)<\infty$ でも $p,q$ を結ぶcausalな測地線が存在しないことがある。
- $\tau$ が連続でないことがある。
下図は $\mathbb{R}^2$ から斜線部を取り除いた開部分多様体に適当なLorentz計量を入れた時空である。
計量が $g=-dt^2+dx^2$ のとき、$\tau(p,q)=2$ だが $p,q$ を結ぶcausalな測地線は存在しない。
計量が $g=\frac{1}{x^2+t^2}(-dt^2+dx^2)$ のとき、$\tau(p,q)=\infty$ である。
計量が $g=\frac{1}{(1+x)^2}(-dt^2+dx^2)$ のとき、$\tau(p,q)<\infty$ であるが、$q\le q'$ となる任意の $q'$ に対して、$\tau(p,q')=\infty$ となるから $\tau$ は不連続である。