因果的過去、未来に関する基本的な事項
ここでは $I^\pm$ と $J^\pm$のそれぞれの性質とこれらの関係性についていくつかの事項をまとめる。
$<<$ はopenである。すなわち、$p<< q$ であるとき、適当な $p$ の近傍 $U$ と適当な $q$ の近傍 $V$ があり、任意の $p'\in U,\ q'\in V$ に対して、$p'<< q'$ が成り立つ。
$p,q$ を結ぶ時間的曲線を $\alpha$ とし、$p,q$ の凸近傍をそれぞれ $C,D$ とする。
$C\cap\alpha$ の点で $p$ の未来にあるものを一つ選び $p^+$ とし、$D\cap\alpha$ の点で $q$ の過去にあるものを一つ選び $q^-$ とする。
$U:=C\cap I^-(p^+),\ V:=D\cap I^+(q^-)$ とすると、作り方から $U,V$ は望みの性質を持つ。
$(1)\ \overline{I^\pm}(p)=\overline{J^\pm}(p),\ (2)\ {\rm int}J^\pm(p)=I^\pm(p),\ (3)\ \partial J^\pm(p)=\partial I^\pm(p)$
$(1)\ \overline{I^\pm}(p)=\overline{J^\pm}(q)$ の証明
$I^+(p)\subset J^+(p)$ より $\overline{I^+}(p)\subset\overline{J^+}(p)$ である。
逆の包含関係を示す。
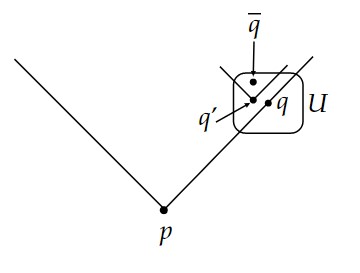
$q\in \overline{J^+}(p)$ とする。
$q$ の任意に小さい近傍を $U$ とすると、$q\in \overline{J^+}(p)$ であるから、$U$ は $q'\in J^+(p)$ となる点 $q'$ を含む。
任意の $\bar{q} \in U\cap I^+(q')$ に対して、$\bar{q}\in I^+(J^+(p))=I^+(p)$ であり、$U$ は任意に小さく取れるから $q$ は $I^+(p)$ の点列の集積点となり得る。
よって $\overline{I^+}\supset\overline{J^+}$ である。
$(2)\ {\rm int}J^\pm(p)=I^\pm(p)$ の証明
$I^+(p)$ は開集合であり、$I^+(p)\subset J^+(p)$ であるから、$I^+(p)\subset {\rm int}J^+(p)$ である。
逆の包含関係を示す。
$q\in {\rm int}J^+(p)$ とすると、$q$ の近傍 $U$ で $q\in U\subset {\rm int}J^+(p)$ となるものが存在する。
任意の $q'\in U\cap I^-(q)$ に対して、$q'\in J^+(p)$ であるから、$q\in I^+(q')\subset I^+(J^+(p))=I^+(p)$ である。
$(3)\ \partial J^\pm(p)=\partial I^\pm(p)$ の証明
(1),(2)と $\partial S=\overline{S}\backslash{\rm int}S$ より明らかである。
次の命題は因果構造論において非常に基本的でかつ重要な命題であり、因果関係の基本定理とも呼ぶべきものである。
$p<< q,\ q< r\Rightarrow p<< r$
$p< q,\ q<< r\Rightarrow p<< r$
$p<< q,\ q< r\Rightarrow p<< r$を示せば十分である。$\alpha$を$p,q$を結ぶtimelike曲線、$\beta$を$q,r$を結ぶcausal曲線とする。$\bar\beta$はコンパクトであるから、有限個の(測地的)凸近傍$\{N_1,N_2,\cdots,N_n\}$で覆うことができる。ここで各$N_i$は適当な凸近傍$C_i$に含まれ、かつ相対コンパクトであるとしてよい。
$y_1\in\beta\cap \overline{N_1}$とし、$a\in\alpha\cap N_1$と1つ取る。$C_1$に$a$を中心とした正規座標$\{x^0,x^1,\cdots,x^n\}$を入れる。$f(x):=-(x^0)^2+(x^1)^2+\cdots+(x^n)^2$とすると、$a<< r$であるから、$f(r)<0$である。$\beta\cap\overline{N_1}$の未来向きの接ベクトルを$T$とすると、$T(f)=2(-T^0x^0+T^1x^1+\cdots+T^nx^n)$であり、$T$はcausalであるから、$T(f)\le0$である。よって$f(y_1)<0$であるから、$a$と$y_1$を結ぶ$N_1$に含まれたtimelike測地線が$\overline{ay_1}$が存在する。$\alpha$の$p$から$a$までの部分を$\alpha'$とすると、$\alpha'\cup\overline{ay_1}$は$p$と$y_1$を結ぶ区分的なめらかなtimelike曲線であり、$p<< y_1$である。$y_1=r$のときはこれで証明は終わりである。$y_1\ne r$のときは$\beta'$を$\beta$の$y_1$から$r$への部分として、$\overline{ay_1}\cup\beta'$に対してこれまでの議論を有限回繰り返せばよい。
この命題の自明な系として次が得られる。
$J^\pm(I^\pm(p))=I^\pm(J^\pm(p))=I^\pm(p)$
