Distinguishing時空
causal時空には閉causal曲線は定義より存在しないが、"ほとんど閉じた"causal曲線が存在する可能性はある。
すなわちある点 $p$ と $p$ に任意に近い点 $q$ を結ぶcausal曲線が存在する可能性がある。
このとき、ある点に対してどんなに小さな近傍をとってもその中でのその点の未来、過去が時空全体での未来、過去の区別と一致しないことが起きる。
このようなことを規制するための性質がDistinguishing時空の定義である。
Distinguishing時空の定義として同値な特徴づけが3つある。
これらの同値性は定義を述べてから証明する。
時空 $(M,g)$ がfuture (resp. past) distinguishing(未来区別、過去区別)であるとは、次の同値な3つの条件を満たすときを言う。
任意の $p\in M$ と任意の近傍 $U(\ni p)$ に対して、$U$ に含まれる $p$ の近傍 $V$ があり、任意の未来向き(resp. 過去向き)causal曲線 $\gamma:[0,1]\rightarrow M$ で $\gamma(0)=p,\gamma(1)\in V$ となるものが、$\gamma([0,1])\subset V$ となるときをいう。
任意の $p\in M$ と任意の近傍 $U(\ni p)$ に対して、$U$ に含まれる $p$ の近傍 $V$ があり、$J^+(p,V)=J^+(p)\cap V$ (resp. $J^-(p,V)=J^-(p)\cap V$)が成り立つ。
$I^+(p)=I^+(q)$ (resp. $I^-(p)=I^-(q)$) ならば、$p=q$
$(1)\Rightarrow(2)$ は自明である。
${\rm non} (3)\Rightarrow {\rm non} (1)$
$p\ne q$ かつ $I^+(p)=I^+(q)$ と仮定する。
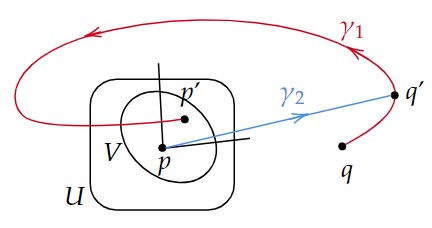
$U\ni p$ で $q\notin\bar{U}$ となる $p$ の近傍を任意に1つ取る。
さらに任意に $V\subset U,\ p\in V$ となる近傍 $V$ を1つ取る。
任意の $p'\in I^+(p,V)$ に対して、$I^+(p)=I^+(q)$ であるから、$q$ から出て $p'$ に至る未来向きの時間的曲線 $\gamma_1$ が存在する。
$q'\in\gamma_1,\ q'\notin\gamma_1\cap U$ となる点 $q'$ に対して、$I^+(p)=I^+(q)$ であるから、$p$ から出て $q'$ に至る未来向きの時間的曲線 $\gamma_2$ が存在する。
$\gamma:=\gamma_1\cup\gamma_2$ は $p$ から出て $p'\in V$ に至る時間的曲線であり、作り方から明らかに $V$ に含まれない。
${\rm non} (1)\Rightarrow {\rm non} (3)$
ある点 $p\in M$ に関して(1)が成り立たないとする。
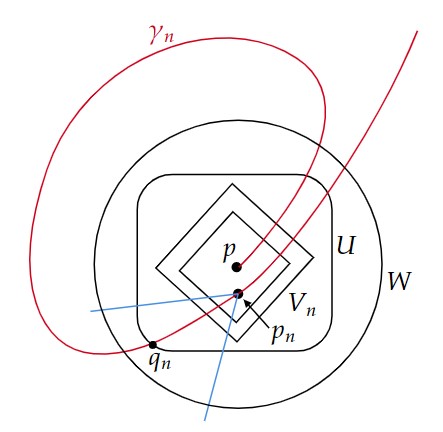
$W\ni p$ を $p$ の凸近傍とし、$U\ni p$ を $W$ に含まれる相対コンパクトな $p$ の近傍とする。
$p$ の近傍の列 $\{V_n\}$ で $U\supset V_n\supset V_{n+1}\ni p,\ \bigcap_n V_n=\{p\}$ かつ $\overline{V}_n$ がコンパクトで $U$ の中で因果的凸であるようなものが存在する。
$p$ に関して(1)が成り立たないから、$p$ から出てさらに $V_n$ からも出て $V_n$ に戻ってくる延長不可能な因果的曲線 $\gamma_n:[0,\infty)\rightarrow M,\ \gamma_n(0)=p$ が存在する。
$V_n$ は $U$ の中で因果的凸であるから $\gamma_n$ は $U$ に含まれない。
$q_n\in \gamma_n\cap\partial U$ を一つ選び点列 $\{q_n\}\in\partial U$ を定める。
ただし、$q_n=\gamma_n(s_n),\ s_n>0$ とする。
さらに、$p_n=\gamma(t_n)\in\gamma_n\cap V_n,\ t_n>s_n>0$ を一つ選び点列 $\{p_n\}\in V_n$ を定める。
このとき $q_n\rightarrow q\in\partial U,\ p_n\rightarrow p$ である。
また $q_n\in J^-(p_n,W)$ であり、$W$ は凸近傍であるから $q\in J^-(p,W)$ である。
よって $I^+(p)\subset I^+(q)$ である。
任意の $q'\in I^+(q)$ に対して、十分大きい $n$ があり、$q_n\in I^-(q')$ となるから $p<< p_n<< q'$ となり、$I^+(p)\supset I^+(q)$ である。
よって $I^+(p)=I^+(q),\ p\ne q$ である。
${\rm non} (1)\Rightarrow {\rm non} (2)$
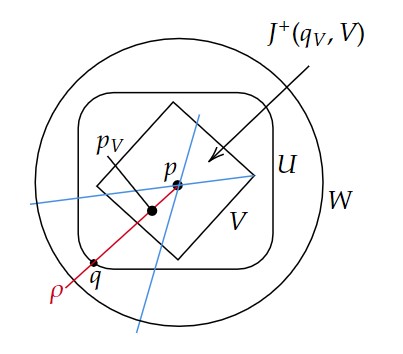
$p\in U\subset W,\ q\in\partial U$ を上の証明における $U,W,q$ とする。
(2)を満たす近傍 $V(\subset U)$ が存在すると仮定して矛盾を導く。
$q\in J^-(p,W)$ であり、$W$ は凸近傍であるから、$p,q$ を結ぶ $W$ に含まれる時間的測地線 $\rho$ がただ一つ存在する。
このとき、$q_V\in (V\cap\rho)\backslash{p}$ を任意に取ると、$I^+(p)=I^+(q_V)$ である(なぜなら、$I^+(p)\subset I^+(q_V)$ は $q_V$ の作り方から自明であり、(1)を否定している仮定だから、$I^+(p)=I^+(q)$ であり、かつ$q_V\in I^+(q)$ より $I^+(q_V)\subset I^+(q)=I^+(p)$ であるから )。
しかし $U$ は凸近傍であるから $J^+(p,U)\ne J^+(q_V,U)$ であり、特に $J^+(p,V)\not\supset I^+(q_V,V)$ である。
一方、$I^+(q_V,V)\subset I^+(q_V)\cap V=I^+(p)\cap V\subset J^+(p)\cap V$ である。
今、$J^+(p)\cap V=J^+(p,V)$ であるから矛盾である。
上の定義(1)で $\gamma(1)$ は $V$ の点としか言ってないが $\gamma(0)$ は $p$ でなければならないことに注意。
この後にあるstrongly causal時空の定義では $\gamma(0)\ne p$ でもよい。
$\mathbb{R}\times R^2$ に計量 $ds^2=(\cosh^2t-1)(-dt^2+dx^2)+2dtdx+dy^2$ を入れる。
ただし、$t$ は $\mathbb{R}$ の座標で、$x,y$ は $R^2$ の標準的な直交座標である。
この $R^2$ に同値類 $(x,y)\sim(x',y')\Leftrightarrow (x,y+1)=(x',y')\ {\rm or}\ (x+1,y+\alpha)=(x',y'),\ \alpha\in\mathbb{R}\backslash\mathbb{Q}$ を定義し、これによる商時空 $\mathbb{R}\times T^2$ を考える。
これは $x=0$ と $x=1$ を $y$ 方向に $\alpha$ ずらして同一視しているため、$t={\rm const.}$ 面において、$x-$曲線は閉曲線にはならないが $T^2$ の中で稠密である。
特に $t=0$ での $T^2$ において $x-$曲線はnull測地線であり、明らかにdistinguishingでない。
しかし、$T^2|_{t=0}$ の誘導計量は退化しているため、$T^2|_{t=0}$ 中の閉曲線はすべてtimelikeではありえない。
また $T^2|_{t\ne0}$ はspacelike超曲面である。従って、causal時空である。
distinguishing時空は体積関数によって特徴づけることができる。
時空 $(M,g)$ がpast (resp. future) distinguishingであることと、$t^-$ (resp. $t^+$) が一般化time functionであることは同値である。
一般に $I^-(p)\subset I^-(q)$ であるとき、点列 $\{p_n\}\in I^-(p)$ で $\lim p_n=p$ となるものを取ると、$\gamma_n:[0,1]\rightarrow M$ で $q=\gamma_n(0),p_n=\gamma_n(1)$ となるtimelike曲線が存在し、$\gamma_n$ の極限曲線 $\gamma$ はtimelike曲線である。
任意の $p'\in I^-(p)$ に対して、$I^+(p')\cap I^-(p)$ は無限個の $p_n$ を含むから $p'\in I^-(\gamma([0,1]))$ である。
従って、$I^-(p)\subset I^-(\gamma([0,1]))\subset I^-(q)$ となる。
distinguishing時空でないとすると、$p\ne q$ で $I^-(p)=I^-(q)$ となる $p,q\in M$ が存在する。
上の議論から $I^-(p)\subset I^-(\gamma([0,1]))\subset I^-(q)$ となる。
従って、$I^-(p)= I^-(\gamma([0,1]))= I^-(q)$ となるから、$t^-$ は $\gamma$ 上で一定となり一般化time functionではない。
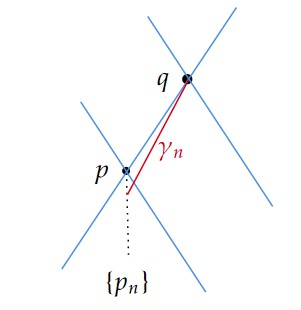
$t^-$ が一般化time functionでないとすると、$p<< q$ で $t^-(p)=t^-(q)$ となる $p,q\in M$ が存在する。
このとき、$I^-(p)=I^-(q)$ を示せばよい。
$I^-(p)\subset I^-(q)$ は自明だから、逆を示す。
$I^-(q)$ のほとんど全ての点が $I^-(p)$ に含まれるから、点列 $\{q_n\}\subset I^-(p)\cap I^-(q)$ で $\lim q_n=q$ となるものが存在する。
構成より $I^-(q_n)\subset I^-(p)$ であり、$I^-(q)=\bigcup_nI^-(q_n)$ であるから、$I^-(q)\subset I^-(p)$ となる。
以下はdistinguishing時空の顕著な結果である。
$(M_1,g_1),(M_2,g_2)$ を2つのLorentz多様体とし、$(M_1,g_1)$ はdistinguishing時空であるとする。
微分同相写像 $f:M_1\rightarrow M_2$ が任意の $p,q\in M_1$ に対して、$p\le q$ ならば $f(p)\le f(q)$ となるとき、$(M_2,g_2)$ はdistinguishingであり、適当な関数 $\rho\in C^0(M_1)$ があり、$f^\ast g_2=e^{2\rho}g_1$ が成り立つ。
