擬極限曲線

　因果構造の考察においてcausal曲線の族を考えることは有用である。
causal曲線の列が適当な意味においてcausal曲線に収束する場合は特に特に便利である。

区分的滑らかなcausal曲線の列がある場合、適当な意味でその極限を考えたい。
このとき、その極限も区分的滑らかな曲線として存在すれば便利である。
このような議論を可能にする道具として極限点列(limit sequence)と擬極限曲線(quasi limit curve)である。
下図を使って感覚的に述べると、極限点列はあるcausal曲線の列 $\{\alpha_n\}$ の”極限”を隣接する2点が十分近い点列で近似したもの（赤点）であり、その点達を測地線で結んでできる区分的滑らかなcausal曲線が擬極限曲線である（青線）。

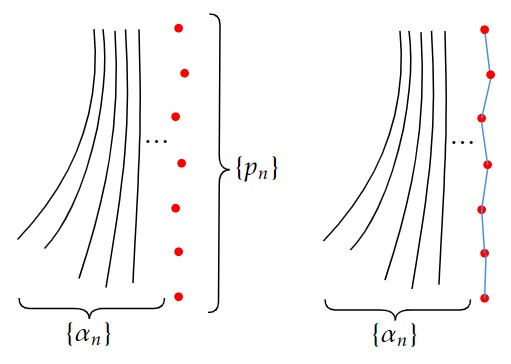
以下詳細に構成を述べる。
まず擬極限曲線が存在するために考える曲線列を次の2つの条件を満たすものに制限して考える。
1つ目は曲線列のそれぞれの曲線の初期位置が収束することであり、2つ目は曲線列が一点に収束しないことである。
すなわち曲線列 $\{\alpha_n\}:[0,b_n)\rightarrow M$ に対して、2つの条件

(i) $\lim_n\alpha_n(0)=p\in M$

(ii) $p$ のある近傍 $V$ が存在し、$\alpha_m([0,b_m))\subset V$ となる $m$ は有限個である

を考える。
（下図は一点に収束する曲線列の例）

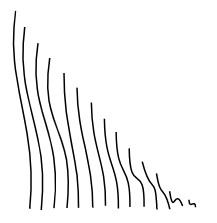
次にこの条件を満たす曲線列に対して、極限点列を構成する。
時空 $(M,g)$ の凸近傍による被覆（凸被覆,convex covering）を任意に一つ取りこれを $\mathfrak{R}$ とする。
$\mathfrak{R}$ の局所有限な細分 $\mathfrak{R}'$ を一つ取る（時空はパラコンパクトであるからこれは常に可能である）。
さらに、任意の $C'\in\mathfrak{R}'$ に対して、ある $C\in\mathfrak{R}$ があり、$C'\subset C$ かつ $C'$ は $C$ に関して相対コンパクトであると仮定してよい。

初めに $p_0=p\in C_1'\in\mathfrak{R}'$ として、$q_n^{(1)}:=\alpha_n\cap\partial C_1'$ とする（$\alpha_k\cap\partial C_1'=\emptyset$ となる $k$ は有限個なのでそれは除く）。
$\partial C_1'$ はコンパクトなので必要なら部分列を取れば、$q_n^{(1)}\rightarrow p_1\in\partial C_1'$ となる。
またこのとき、$p_0,p_1\in \overline{C_1'}$ であり、ある $C_1\in\mathfrak{R}$ があり、$C_1'\subset C_1$ である。
$C_1$ は凸近傍であり、$\alpha_n(0)\le q_n^{(1)}$ であるから、$p_0\le p_1,\ p_0,p_1\in C_1$ である。
（下図参照）

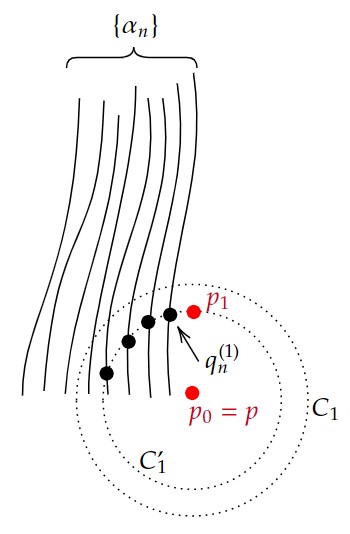
次に $k\geq1$ に対して $p_k\in C_{k+1}'\in\mathfrak{R}'$ とする。
ただし、このとき

$p_k$ を含む $\mathfrak{R}'$ の元は有限個であり、その有限個の中からこれまでに選ばれた回数が最小のものを選ぶ。$\cdots(\ast)$

このとき次の2つの場合があり得る。

(i) $C'_{k+1}$ から出ていく $\alpha_m$ が有限個の場合

$q^{(k+1)}_n=\alpha_n\cap\partial C'_{k+1}$ とおくと（$\partial C'_{k+1}$ と交わらない有限個は除く）、$q^{(k+1)}_n\rightarrow p_{k+1}\in\partial C'_{k+1}$ となる。
特にこのとき、$p_k\le p_{k+1}$ である。

(ii) $C'_{k+1}$ から出ていく $\alpha_m$ が無限個の場合

有限個を除いて $\{\alpha_n(b_n)\}\in \overline{C'_{k+1}}$ であるから、$\alpha_n(b_n)\rightarrow q\in \overline{C'_{k+1}}$ である。
$q\ne p_k$ のとき、$p_{k+1}:=q$ とおく。
このとき、$p_k\le p_{k+1}$ である。

以上の処方により得られる点列 $p=p_0< p_1<\cdots< p_k<\cdots$ が極限点列である。
さらに極限点列 $\{p_k\}$ が無限列のときは $\{p_k\}$ は収束しないことが以下のように分かる。

もし $p_k\rightarrow q$ なら $q\in C'\in\mathfrak{R}'$ となる $C'$ が存在し、$C'$ は $\{p_n\}$ の点を無限個含む。
$\mathfrak{R}'$ は局所有限であるから、$C'\cap D\ne\emptyset$ となる $D\in\mathfrak{R}'$ は有限個である。
それらを $\{C'=C'_0,C'_1,\cdots,C'_l\}$ とする。
$C'$ に含まれる各 $\{p_n\}$ に対して、$C_i$ のどれかが選ばれているから、少なくとも一つは無限回選ばれている。
もし $C'$ が無限回選ばれているなら、$\partial C'$ に無限個の部分列 $\{p_{k_n}\}$ が存在し、$p_{k_n}\rightarrow p'\in\partial C'$ となるが、これは $p_k\rightarrow q\in C'$ に矛盾する。
従って、$C'$ が無限回選ばれていることはない。
しかし、これは選び方の基準 $(\ast)$ に矛盾する。

以上により以下の定理を得る。