Strongly Causal時空
時空の任意の点の十分小さい近傍 $U$ において、$U$ の中で因果的凸となる近傍 $V$ は存在する。
しかし、$U$ を任意に取った場合は因果的凸近傍が存在するとは限らない。
これを保障するのがstrongly causal時空である。
また、“ほとんど閉じた”causal曲線を完全に規制する条件でもある。
時空 $(M,g)$ がある点 $p\in M$ においてstrongly causalであるとは、次の同値な条件のいずれかを満たす時を言う。
$p$ の任意の近傍 $U$ に対して、$p$ の適当な近傍 $V(\subset U)$ で $M$ において因果的凸であるものが存在する。
$p$ の任意の近傍 $U$ に対して、適当な近傍 $V(\ni p)$ があり、任意のcausal曲線 $\gamma:[0,1]\rightarrow M$ で $\gamma(0),\gamma(1)\in V$ ならば、$\gamma\subset U$ となる。
任意の $p\in M$ においてstrong causalであるとき、時空 $(M,g)$ はstrong causalであると言う。
$(1)\Rightarrow(2)$ は自明である。
逆に条件(2)が成り立つとする。
$p$ の任意の近傍 $U$ に対して、2つの近傍 $p\in V\subset U'\subset U$ で $V$ が $U'$ の中で因果的凸であるものが存在する。
$U'$ に対して、(2)の条件を満たす近傍として $V$ を取ることが出来る。
このとき $V$ に2つの端点を持つ $M$ のcausal曲線 $\gamma$ は(2)の条件より $U'$ に含まれるが、$V$ は $U'$ の中で因果的凸であるから $\gamma\subset V$ である。
従って、$V$ は $M$ において因果的凸である。
下図はdistinguishingだがstrong causalでない時空の例である。
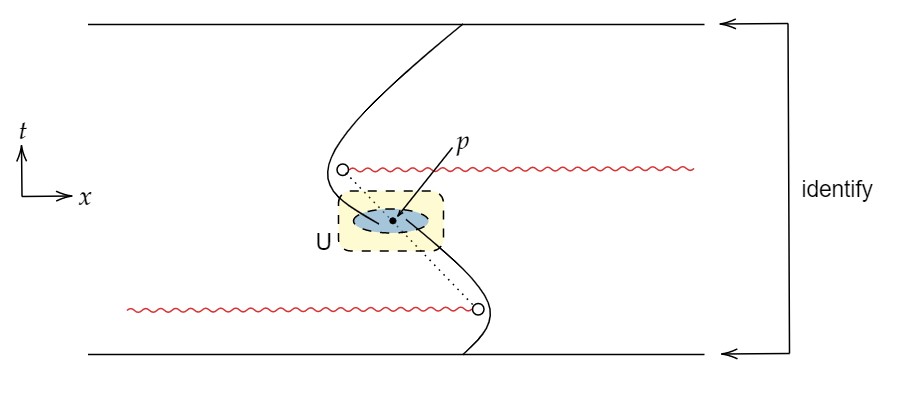
strong causal時空にはAlexandorv位相による特徴付けがある。
時空 $(M,g)$ において、部分集合族
$$
\begin{align}
\mathcal{B}_A:=\{I^+(p)\cap I^-(q);\ p,q\in M\}
\end{align}
$$
が開基となって定める位相をAlexandorv位相(Alexandorv topology)という。
位相空間 $(X,O)$ の基とは $X$ 部分集合族 $B$ で $X$ の任意の開集合が $B$ の部分族の和集合となるときを言う。
時空 $(M,g)$ に関して以下は同値である。
- $(M,g)$ はstrong causal時空である。
- Alexandorv位相は $M$ の元の位相と一致する。
- Alexandorv位相はHausdorffである。
$(1)\Rightarrow(2)$
$\mathcal{B}_A$ がある位相の開基となっていることはすぐにわかる。
さらに $\mathcal{B}_A$ の元は $M$ の元の位相に関して開集合であるから、$M$ の元の位相はAlexandorv位相より細かい。
任意 $x\in M$ と $x$ の任意の近傍 $U\ni x$ に対して、$(M,g)$ はstrong cuausal時空であるから、$x\in V\subset U$ で $<<_V$ と $<<$ が一致するような近傍 $V$ が存在する。
従って、$p,q\in V$ で $p<<_Vx,\ x<<_Vq$ となる2点に対して $q\in I^-(q)\cap I^+(p)\subset U$ となる。
$(2)\Rightarrow(3)$
自明である。
$(3)\Rightarrow(1)$
待遇を取り、(1)の否定から(3)の否定を導く。
ある点 $p$ がstrongly causalでないとする。
$p$ の凸近傍 $W$ を取り、$W$ に対して相対コンパクトな $p$ の近傍 $U\subset W$ を取る。
さらに必要なら $U$ を小さく取り直し、$U$ の中で因果的凸な $p$ の近傍族 $\{V_n\},\ p\in V_n,\ \bigcap_nV_n=\{p\}$ を取る。
十分大きい $n$ と任意の $p_n,r_n\in V_n$ に対して、$p_n$ から出発し $r_n$ に戻ってくる $W$ に含まれない未来向きのcausal曲線を $\gamma_n$ とする。
$U$ は $W$ に対して相対コンパクトだから $q_n\in\gamma_n\cap\partial U$ は必要なら部分列を取れば $q_n\rightarrow q\rightarrow\partial U$ となる。
$W$ は凸近傍であり、$q_n<< r_n$ かつ $r_n\rightarrow_W p$ であるから、$q<<_Wp$ である。
$q_1<< q<< q_2$ となる任意の $q_1,q_2\in M$ に対して、$q_1<< p$ である。
また十分大きい $n$ に対して、$p_n<< q<< q_2$ である。
$p_n$ を $p<<_{V_n}p_n$ となるように取れば、$p_n\in I^+(q_1)\cap I^-(q_2)$ である。
よって、$p$ は $I^+(q_1)\cap I^-(q_2)$ の集積点であるから、$p$ の任意の近傍は $I^+(q_1)\cap I^-(q_2)$ と交わりを持つ。
Strongly causal時空の基礎的な性質として次の2つの命題がある。
strongly causal時空 $(M,g)$ において、延長不可能なcausal曲線 $\gamma:[0,b)\rightarrow M$ がコンパクト集合 $K$ に対して、$\gamma(0)\in K$ であるならば、ある $s\le b$ があり、$t>s$ となる任意の $t$ に対して、$\gamma(t)\notin K$ となる。
結論を否定して矛盾を導く。
結論の否定により、点列 $\{t_n\},\ t_n\rightarrow b$ で $\gamma(t_n)\in K$ となるものが存在する。
$K$ のコンパクト性より必要なら部分列を取り直し $\gamma(t_n)\rightarrow p\in K$ となる。
$\gamma$ は延長不可能でるから別の点列 $\{u_n\},\ u_n\rightarrow b$ で $\gamma(u_n)$ が $p$ に収束しないものが存在しなければならない(もし全ての点列が $p$ に収束すれば定義より延長可能になってしまう)。
必要なら点列の番号を付け替えて、$t_1< u_1< t_2< u_2<\cdots< t_i< u_{i+1}<\cdots< b$ であるとしてよい。
$\gamma(u_n)$ は $p$ に収束しないからある近傍 $U\ni p$ があり、$\gamma(u_n)\notin U$ である。
任意の$p$ の近傍 $V(\subset U)$ に対して、ある $k$ があり、$\gamma(t_k),\gamma(t_{k+1})\in V$ であり、 $\gamma(u_k)\notin U$ である。
これは $p$ がstrongly causalであることに矛盾する。
$(M,g)$ をstrongly causal時空、$K$ をコンパクト部分集合とする。
未来向きのcuasal曲線の列 $\{\alpha_n\}:[0,1]\rightarrow K,\ (\lim\alpha_n(0)=p,\ \lim\alpha_n(1)=q,\ p,q\in K,\ p\ne q)$ に対して、
区分的滑らかな未来向きcausal測地線 $\lambda:[0,1]\rightarrow K,\ \lambda(0)=p,\lambda(1)=q$ で、ある部分列 $\{\alpha_m\}$ があり、$\lim L(\alpha_m)\le L(\lambda)$ となるものが存在する。
$\{\alpha_n\}$ の極限点列を $p=p_0\le p_1\le p_2\le\cdots\le p_n=q$ とする($n=\infty$ だと擬極限曲線が延長不可能になり上の命題よりあり得ない)。
擬極限曲線を $\lambda=\bigcup_{i=0}^{n-1}\overrightarrow{p_ip_{i+1}}$ とする。
このとき、$\overrightarrow{p_ip_{i+1}}\subset K$ でかつある凸近傍 $C_i$ があり $\overrightarrow{p_ip_{i+1}}\subset C_i$ となっているとしてよい。
このとき、部分列 $\{\alpha_m\}$ があり、$\alpha_m(s_{m,i}),\alpha_m(s_{m,i+1})\subset C_i$ となっていて、
$$
\begin{align}
L(\alpha_m([s_{m,i},s_{m,i+1}]))\le L(\overrightarrow{\alpha_m(s_{m,i})\alpha_m(s_{m,i+1})})
\end{align}
$$
である。
ただし、$\overrightarrow{\alpha_m(s_{m,i})\alpha_m(s_{m,i+1})}$ は $\alpha_m(s_{m,i}),\alpha_m(s_{m,i+1})$ を結ぶ未来向き測地線である。
凸近傍内では $L$ は連続であるから、
$$
\begin{align}
\lim_{m\rightarrow\infty}L(\alpha_m)\le L(\lambda)
\end{align}
$$
擬極限曲線がnull測地線となるようなtimelike曲線の列に対しても上の命題は成立することに注意するべきである。すなわち $\lim_{m\rightarrow\infty}L(\alpha_m)=L(\lambda)=0$ である。この例から分かるように有限 $m$ に対しては不等式が成立するとは限らない。
次の命題は2次元の特殊さを示す。
任意の単連結な2次元時空はstrongly causalである。
time separationはRiemann多様体における距離に対応する概念であるが、Lorentz多様体としての等長同型とtime separationが保存されることが一致するのがstrongly causal時空である。
$(M,g),(M',g')$ を次元が同じ時空とし、$(M,g)$ をstrongly causal時空とする。
全射 $f:M\rightarrow M'$ が
$$
\tau(p,q)=\tau'(f(p),f(q)),\ {}^\forall p,q\in M
$$
を満たすならば、$f$ は等長同型写像である。
特に $M=M'$ ならばtime separationが一致するのは計量が一致するときに限る。
ここで、$\tau,\tau'$ はそれぞれ $(M,g),(M',g')$ のtime separationである。
また $f$ に対して連続性の仮定は必要ない。
