Totally Vicious時空
概要
Totally Vicious時空について解説する。
Totally Vicious時空について因果階層において定義のみ説明した。まず因果階層において述べた6つの同値な定義は以下である。
時空$(M,g)$がTotally Viciousであるとは次の同値な条件のいずれかを満たすことである。
(T1) 任意の$p\in M$に対して、$ I^+(p)\cap I^-(p)=M$
(T2) ある$p_0\in M$に対して、$ I^+(p_0)\cap I^-(p_0)=M$
(T3) 任意の$p\in M$に対して、$p$を通る閉timelike曲線(CTC)が少なくとも一つ存在する。
(T4) 任意の$p,q\in M (p\ne q)$に対して、$p$と$q$を結ぶtimelike曲線が少なくとも一つ存在する。
(V1) 任意の$p\in M$に対して、$ J^+(p)\cap J^-(p)=M$
(V2) ある$p_0\in M$に対して、$ J^+(p_0)\cap J^-(p_0)=M$
ここではTotally Vicious時空（以下TV時空）のいくつかの性質について述べる。
Totally Viciousとなるための十分条件
上の定義はもちろん必要十分であるが、上の定義が成り立っているかを任意の時空に対して調べる方法を確立するのは困難である。そこでもう使いやすい十分条件を調べる。
時空$(M,g)$がreflectingでかつ少なくとも１つCTCが存在するならば、TVである。
この定理を証明するために$\overline{I^\pm(p)}$という集合について補題を準備する。
$ \overline{I^+(p)}=\{r\in M;\ I^+(r)\subset I^+(p)\}$
$ T=\{r\in M;\ I^+(r)\subset I^+(p)\}$とする。
(i)$ \overline{I^+(p)}\subset T$を示す。
$ r\in \overline{I^+(p)}$に対して、$ I^+(r)\subset I^+(p)$を示せば良い。
$ r^+\in I^+(r)$に対して、$ I^-(r^+)$は$ r^+$の近傍だから、点列$ \{r_n\},r_n\to r$で大きい$ n$に対して、$ r_n\in I^-(r^+)\cap I^+(p)$となるものがある。よって$ p<< r_n<< r^+$であるから、$ r^+\in I^+(p)$となる。したがって$ I^+(r)\subset I^+(p)$である。
(ii)$ \overline{I^+(p)}\supset T$を示す。
$ T\ni r$を含む任意の近傍$ U$に対して、$ I^+(r,U)$は$ I^+(p)$に含まれるから、$ U\cap I^+(p)\ne\emptyset$となる。よって$ r\in \overline{I^+(p)}$である。
以上の準備から定理１を示すことができる。
$ I^\pm(p_0)=\overline{I^\pm(p_0)}$が示されれば、$ I^\pm(p_0)$はopen & closedなので$ I^\pm(p_0)=M$より$ I^+(p_0)\cap I^-(p_0)=M$となりTVとなる。よって$ I^\pm(p_0)=\overline{I^\pm(p_0)}$を示せばよい。
$ I^\pm(p_0)\subset\overline{I^\pm(p_0)}$は明らかであるから、$ I^\pm(p_0)\supset\overline{I^\pm(p_0)}$を示す。
$ \gamma$をCTCとし、$ \gamma(0)=p_0,\gamma(u)=\gamma(u+1),\gamma(v)>>\gamma(u)\ (v>u)$であるとする。
$ r\in \overline{I^+(p_0)}$とすると、reflectivityより$ p_0\in \overline{I^-(r)}$となるから、補題１より$ I^-(p_0)\subset I^-(r)$である。
$ \gamma(-\epsilon)\subset I^-(r)$より$ I^+(\gamma(-\epsilon))\ni r$となる(ここまではreflectingなら$\gamma$がCTCでなくても常に成り立つ）。
$ \gamma(-\epsilon)=\gamma(1-\epsilon)\in I^+(p_0)$なので、$ r\in I^+(p_0)$となる。
（つまり$ p_0$の過去の未来に$ r$があり、CTCのおかげで$ p_0$の過去が未来にあるから$ r$が$ p_0$の未来にある。）
reflectingという性質は結構いろいろな時空で満たされるので強力である。以下の系が得られる。
時空$(M,g)$の任意の$p\in M$に対して、$J^\pm(p)$が閉であり、さらにCTCが存在するならばTVである。
$ p\in \overline{I^+(q)}(=\overline{J^+(q)})$のとき、仮定より$\overline{J^+(q)}=J^+(q)$であるから、$p\in J^+(q)$である。よって、同様の議論で$ q\in J^-(p)=\overline{I^-(p)}$となるから、reflectingである。よって定理２より主張が従う。
他にも次の便利な応用がある。
定常時空がCTCを持てばTVである。
定常時空はreflectingであるから、系2より従う。
これを使うと与えられた時空がTVであるかどうか判定できることがある。
Gödel宇宙はTVである。
Gödel宇宙の計量はPoincare model based座標において
$$
\begin{align}
ds^2=-\left(dt+\frac{\omega}{2}\frac{r^2d\theta}{1+\frac{K}{4}r^2}\right)^2+\frac{dr^2+r^2d\theta^2}{(1+\frac{K}{4}r^2)^2}+dz^2,
K=-\omega^2/2
\end{align}
$$
と表される。
$t=$一定面上に誘導される計量は
$$
\begin{align}
ds^2&=\frac{dr^2}{(1+\frac{K}{4}r^2)^2}+\left(\frac{r^2}{(1+\frac{K}{4}r^2)^2}-\frac{\omega^2}{4}\frac{r^4}{(1+\frac{K}{4}r^2)^2}\right)d\theta^2+dz^2 \\
&=\frac{dr^2}{(1+\frac{K}{4}r^2)^2}+\frac{r^2(1-\frac{\omega^2}{4}r^2)}{(1+\frac{K}{4}r^2)^2}d\theta^2+dz^2
\end{align}
$$
となるから、$t=$一定面上において、$||\partial_\theta||^2=\frac{r^2(1-\frac{\omega^2}{4}r^2)}{(1+\frac{K}{4}r^2)^2}$である。よって、$\partial_\theta$の積分曲線は閉曲線であり、さらに$2/\omega< r$の領域においてtimelikeである。したがってCTCが存在する。
コンパクト時空
コンパクト時空とTV時空との関係を述る。まずコンパクト時空について基本的なことは以下である。
コンパクト時空$(M,g)$はCTCを持つ。
$M=\bigcup_{p\in M} I^+(p)$であり、コンパクトであることから有限集合$S=\{p_i\}$が存在して、$M=\bigcup_{p_i\in S} I^+(p_i)$となる。今$I^+(p_1)$が他の$I^+(p_i)$には含まれないとする（もし含まれるなら$S$から$p_1$を取り除けばよい）。よって$p$は他の$I^+(p_i)$には含まれない。従って$p_1\in I^+(p_1)$でなければならない。
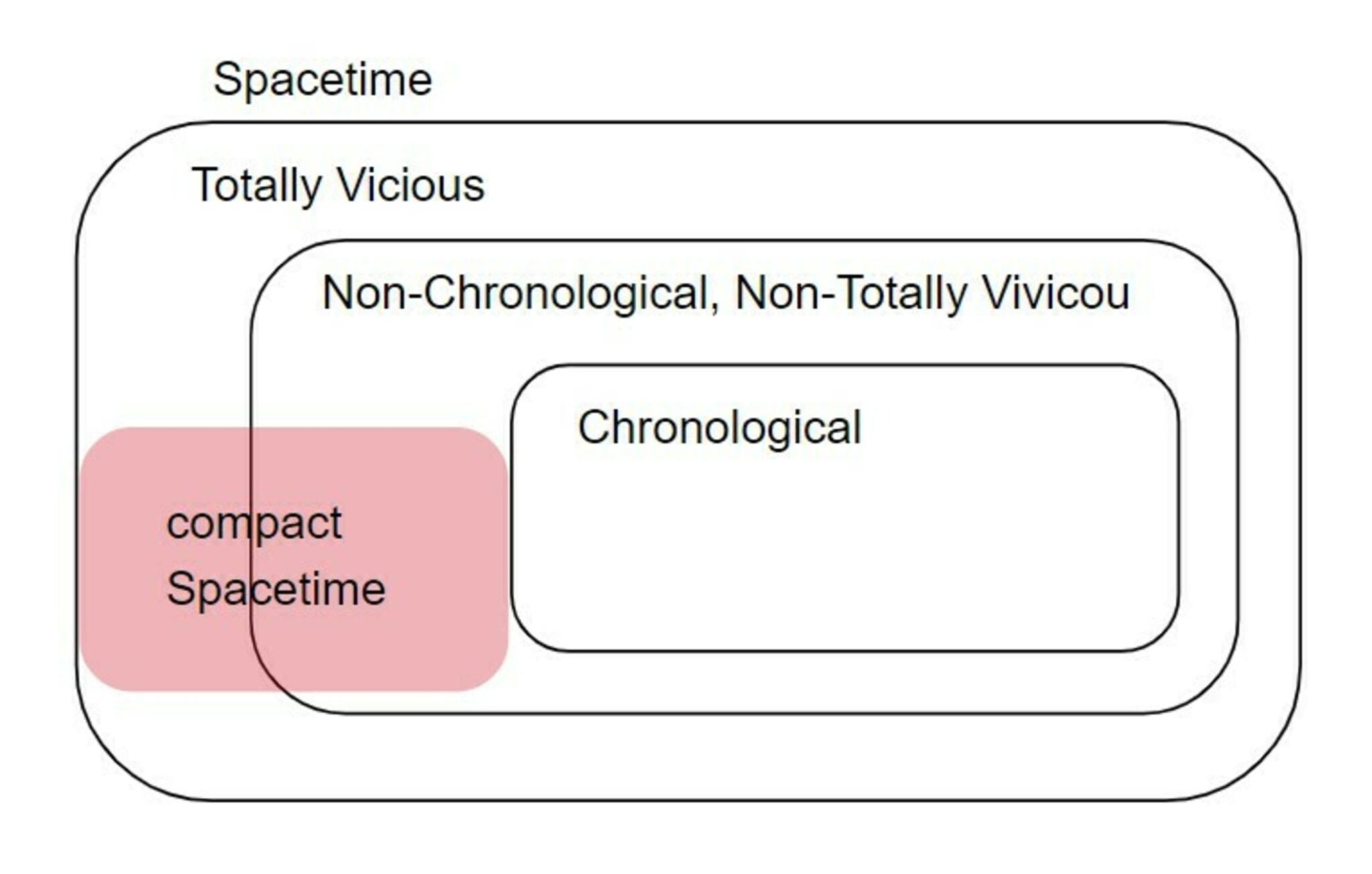因果構造の包含関係
このことからコンパクト時空はchronological時空ではない。従って、Non-chronological Non-TV時空またはTV時空のどちらかである。コンパクトでNon-chronological Non-TVな時空の例として以下のものがある。
$(\mathbb{R}^2,\{t,x\})$に次の計量を定める。
$$
g=\cos^2x(-dt^2+dx^2)+2\sin x dtdx
$$
これを$(t,x)\sim(t+1,x),(t,x)\sim(t,x+2\pi)$という同値類で割った2次元Lorentzianトーラス$(T^2,g)$を考える。
$$
g(\partial_t,\partial_t)=-\cos^2x,\ \nabla_{\partial_t}\partial_t=-\frac{\sin x\cos x}{\sin^2 x+\cos^4 x}(\sin x\partial_t+\cos^2 x\partial_x)
$$
であるから、$x=\pm\frac{\pi}{2}$において、$t-$曲線はnull測地線である。
また光円錐は下図のようになっている。
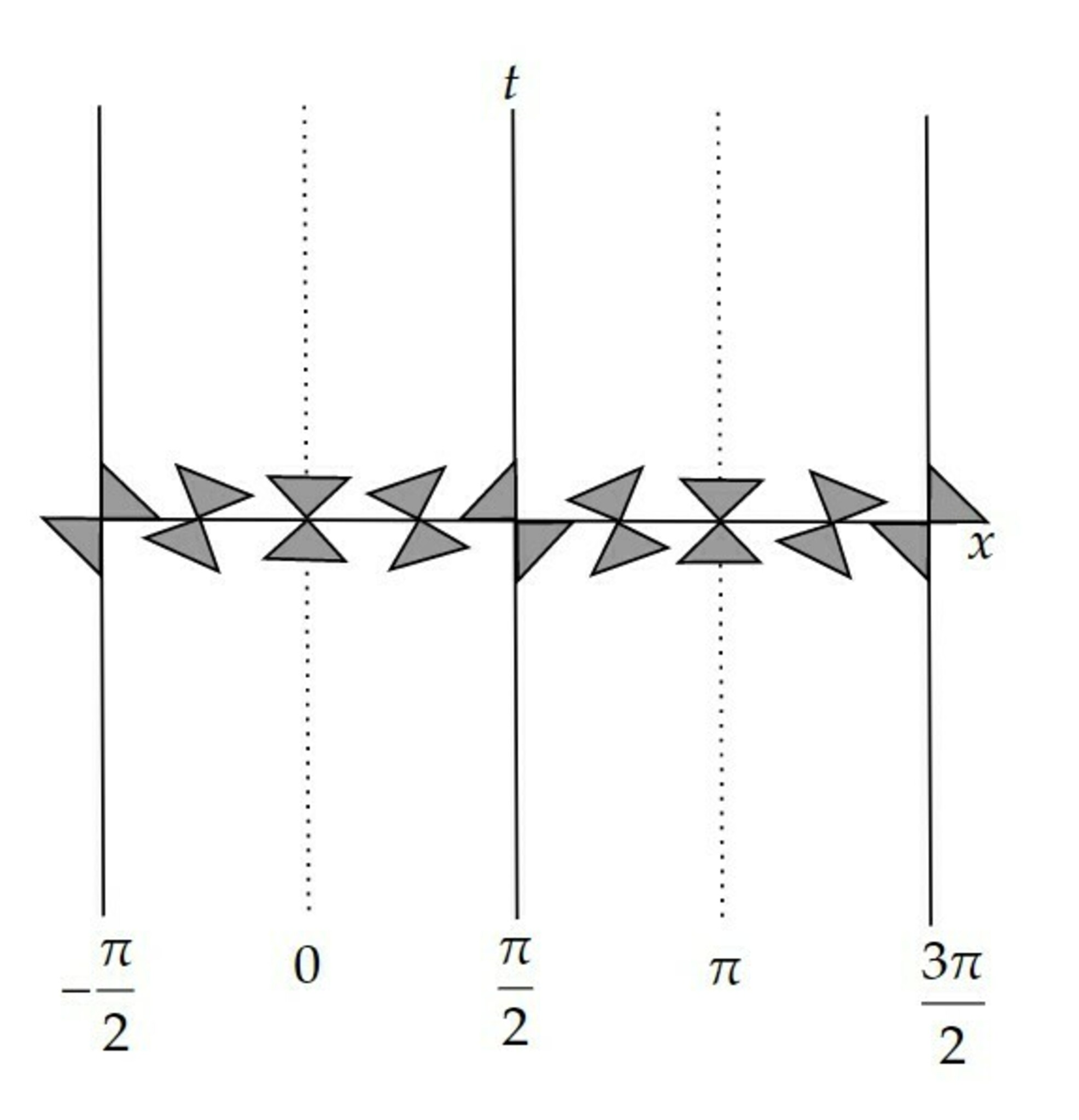(M,g)の光円錐
これより$p=(0,0)$に対して、$I^+(p)\subset \{(t,x);\ |x|<\pi/2\}$となることが分かるので、$(T^2,g)$はTVではない。
また$I^-(p)=M$が成り立つ。
上の例があることからコンパクト時空がいつTVとなるかという問題意識が生じる。TV時空がreflectingであることは自明なので、定理２、命題３を合わせると直ちに次が従う。
コンパクト時空$(M,g)$がreflectingであることと、TVであることは同値である。
homogeneous時空はreflectingであるから次の系を得る。
コンパクトなhomogeneous時空はTVである。
