Bianchi分類
概要
3次元実リー環の(同型を除いた)分類をBianchi分類という。
Bianchi分類とは3次元実リー環の(同型を除いた)分類である。
3次元実リー環は11種類に分類され、そのうち2つは非可算個の族である。
この記事ではBianchi分類の手法と結果を記載する。
$\mathfrak{g}$ を3次元実Lie環とし、$\{X_i\}$ を基底とする。
構造定数 $C^i_{jk}$ を $[X_i,X_j]=\sum_iC^i_{jk}X_i$ により定める。
基底の取り換えは正則な行列 $T$ により $X'_i=\sum_jX_jT^j_i$ で与えられ、このとき構造定数は $C'^i_{jk}=\sum_{a,b,c}(T^{-1})^i_aT^b_jT^c_kC^a_{bc}$ と変換する。
この変換で移り合う構造定数は同値なリー環を定める。
従ってLie環の同型類を考えることは同値な構造定数の類を考えることに帰着される。
3次元実Lie環の構造定数 $C^i_{jk}$ を分類するために構造定数の表示を書き換える。
3次元実リー環の構造定数 $C^i_{jk}$ は対称行列 $N^{ij}(=N^{(ij)})$、3次元実ベクトル $a_i$、完全反対称テンソル $\epsilon_{ijk}(=\epsilon_{[ijk]})$ を用いて
$$
\begin{align}
C^i_{jk}=\sum_lN^{il}\epsilon_{ljk}+a_j\delta^i_k-a_k\delta^i_j
\end{align}
$$
で与えられる。
またこのときJocobi恒等式は
$$
\begin{align}
\sum_jN^{ij}a_j=0
\end{align}
$$
と同値である。
まず完全反対称テンソル $\epsilon_{ijk}(=\epsilon_{[ijk]})$ を用いて、
$$
\begin{align}
\tilde{C}^{ij}&=\frac{1}{2}\sum_{a,b}C^i_{ab}\epsilon^{jab},\\
\tilde{C}&=\begin{pmatrix}C^1_{23} & C^1_{31} & C^1_{12} \\ C^2_{23} & C^2_{31} & C^2_{12} \\ C^3_{23} & C^3_{31} & C^3_{12}\end{pmatrix},
\end{align}
$$
を定義する。
次に $\tilde{C}$ を対称部分と反対称部分へ分解する。
$$
\begin{align}
\tilde{C}&=S(\tilde{C})+A(\tilde{C}),\\
S(\tilde{C})&=\frac{1}{2}(\tilde{C}+{}^t\tilde{C}),\\
A(\tilde{C})&=\frac{1}{2}(\tilde{C}-{}^t\tilde{C}).
\end{align}
$$
$N:=S(\tilde{C})$ と置くと、
$$
\begin{align}
N^{ij}=\tilde{C}^{(ij)}=\sum_{a,b}\frac{1}{4}(C^i_{ab}\epsilon^{jab}+C^j_{ab}\epsilon^{iab})
\end{align}
$$
である。
また
$$
\begin{align}
A(\tilde{C})=\frac{1}{2}\begin{pmatrix}
0 & C^1_{31}+C^2_{32} & -C^1_{21}-C^3_{23}\\
-C^1_{31}-C^2_{32} & 0 &C^2_{12}+C^3_{13}\\
C^1_{21}+C^3_{23} & -C^2_{12}-C^3_{13} & 0
\end{pmatrix}
=\frac{1}{2}\begin{pmatrix}
0 & \sum_aC^a_{3a} & -\sum_aC^a_{2a}\\
-\sum_aC^a_{3a} & 0 & \sum_aC^a_{1a}\\
\sum_aC^a_{2a} & -\sum_aC^a_{1a} & 0
\end{pmatrix}
\end{align}
$$
であるから、$a_i=\frac{1}{2}\sum_aC^a_{ia}$ と置くと
$$
\begin{align}
A(\tilde{C})=\frac{1}{2}\begin{pmatrix}
0 & a_3 & -a_2\\
-a_3 & 0 & a_1\\
a_2 & -a_1 & 0
\end{pmatrix}
\end{align}
$$
と書ける。
従って、
$$
\begin{align}
\tilde{C}^{ij}&=N^{ij}+\sum_k\epsilon^{ijk}a_k,\\
\frac{1}{2}\sum_{k,l}C^i_{kl}\epsilon^{jkl}&=N^{ij}+\sum_k\epsilon^{ijk}a_k,\\
\therefore\ C^i_{jk}&=\sum_lN^{il}\epsilon_{ljk}+\sum_{l,m}\epsilon^{ilm}a_m\epsilon_{ljk},\\
&=\sum_lN^{il}\epsilon_{ljk}+\sum_{m}(\delta^i_j\delta^m_k-\delta^i_k\delta^m_j)a_m,\\
&=\sum_lN^{il}\epsilon_{ljk}+a_j\delta^i_k-a_k\delta^i_j
\end{align}
$$
となる。
さらにJacobi恒等式は
$$
\begin{align}
\sum_l(C^l_{jk}C^m_{il}+C^l_{ki}C^m_{jl}+C^l_{ij}C^m_{kl})=0
\end{align}
$$
と同値である。
以下の少し長いをすると、
$$
\begin{align}
\sum_lC^l_{jk}C^m_{il}&=(N^{la}\epsilon_{ajk}+a_j\delta^l_k-a_k\delta^l_j)(N^{ma}\epsilon_{ail}+a_i\delta^m_l-a_l\delta^m_i),\\
&=N^{la}\epsilon_{ajk}N^{mb}\epsilon_{bil}+N^{la}\epsilon_{ajk}a_i\delta^m_l-N^{la}\epsilon_{ajk}a_l\delta^m_i\\
&+a_j\delta^l_kN^{ma}\epsilon_{ail}+a_j\delta^l_ka_i\delta^m_l-a_j\delta^l_ka_l\delta^m_i\\
&-a_k\delta^l_jN^{ma}\epsilon_{ail}-a_k\delta^l_ja_i\delta^m_l+a_k\delta^l_ja_l\delta^m_i\\
&=(N^{la}\epsilon_{ajk}+a_j\delta^l_k-a_k\delta^l_j)(N^{ma}\epsilon_{ail}+a_i\delta^m_l-a_l\delta^m_i),\\
&=N^{ma}\epsilon_{ajk}a_i-N^{la}\epsilon_{ajk}a_l\delta^m_i\\
&+a_jN^{ma}\epsilon_{aik}-a_kN^{ma}\epsilon_{aij},\\
\sum_lC^l_{ki}C^m_{jl}&=N^{la}\epsilon_{aki}a_j-N^{la}\epsilon_{aki}a_l\delta^m_j\\
&+a_jN^{ma}\epsilon_{aji}-a_kN^{ma}\epsilon_{ajk},\\
\sum_lC^l_{ij}C^m_{kl}&=N^{ma}\epsilon_{aij}a_k-N^{la}\epsilon_{aij}a_l\delta^m_k\\
&+a_iN^{ma}\epsilon_{akj}-a_jN^{ma}\epsilon_{aki},\\
\sum_l(C^l_{jk}C^m_{il}+C^l_{ki}C^m_{jl}+C^l_{ij}C^m_{kl})
&=a_jN^{ma}\epsilon_{aik}+a_kN^{ma}\epsilon_{aji}+a_iN^{ma}\epsilon_{akj}-a_lN^{la}(\epsilon_{ajk}\delta^m_i+\epsilon_{aki}\delta^m_j+\epsilon_{aij}\delta^m_k)
\end{align}
$$
となる。
今、$i\ne j\ne k,\ m=i$ または、$i=k\ne j$ の2つの場合を考えれば十分である。
$i=k\ne j$ のときは、$\sum_l(C^l_{jk}C^m_{il}+C^l_{ki}C^m_{jl}+C^l_{ij}C^m_{kl})=0$ であり、$i\ne j\ne k,\ m=i$ のときは、 $\sum_l(C^l_{jk}C^m_{il}+C^l_{ki}C^m_{jl}+C^l_{ij}C^m_{kl})=-2\sum_la_lN^{il}\epsilon_{ijk}$ である。
よって、Jacobi恒等式は $\sum_jN^{ij}a_j=0$ である。
この $N,a$ は上記の基底の変換に関して、 $N'=(\det T)T^{-1}N{}^tT^{-1},\ a'={}^tTa$ と変換する。
従って、3次元実Lie環の分類はこの変換で移り合う $N,a$ の同値類を求める問題に帰着される。
3次元実Lie環は、$||a||=\sqrt{\sum_{i=1}^3 a_i^2}$ と3次対称行列 $N$ の固有値 $N_1,N_2,N_3$ により、以下のように分類される。
また任意の3次元実Lie環はこのいずれかと同型である。
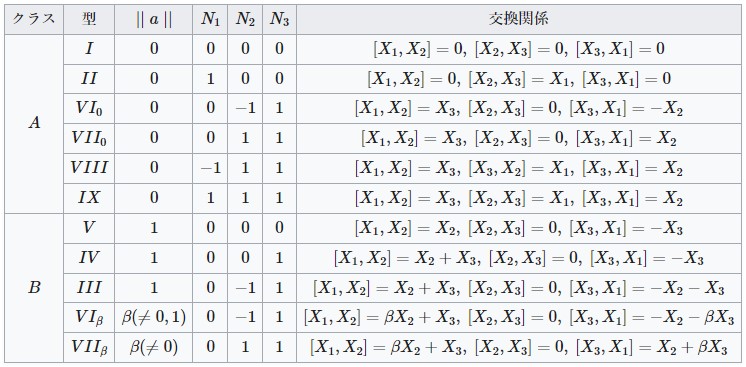 Binachi分類
Binachi分類
まず$||a||=0$のクラス $A$ と $||a||\ne0$ のクラス $B$ の2つの場合がある。
クラス $A$ について:
直交行列 $T_1\in O(3)$ により $N$ を対角化して、$N=(\det T_1){\rm diag}(\lambda_1,\lambda_2,\lambda_3),\ \lambda_i\in\mathbb{R}$ とできる。
さらに $T_2={\rm diag}(\alpha_2\alpha_3,\alpha_1\alpha_3,\alpha_1\alpha_2)$ により変換すると、$N=(\det T_1){\rm diag}(\alpha_1^2\lambda_1,\alpha_2^2\lambda_2,\alpha_3^2\lambda_3)$ とできるから、$\lambda_i=\pm1,0$ としてよい。
固有値の並びも直交行列による変換で入れ替わるので組み合わせと相対的な符号のみ意味がある。
従って、上記の表の結果を得る。
クラス $B$ について:
適当な $SO(3)$ の変換により、$a_1=||a||,a_2=a_3=0$ とできる。
さらに $Na=0$ であるから、2次対称行列 $n$ を用いて、
$$
\begin{align}
N=\begin{pmatrix}
0 &0\\
0& n
\end{pmatrix}
\end{align}
$$
となっている。
さらに直交変換で対角化すると、$N={\rm diag}(0,\lambda_2,\lambda_3)$ となり、クラス $A$ と同様に $\lambda_2,\lambda_3=0,\pm1$ であり、順序は意味がなく、相対的な符号のみ意味がある。
従って、次のいずれかの場合に帰着される。
(i) $\lambda_2=\lambda_3=0$ のとき
$T=\alpha I_3$ の変換で $||a||=1$ とできるので、V型である。
(ii) $\lambda_2=0,\lambda_3=1$ のとき
$T={\rm diag}(\alpha,1,\alpha)$ の変換で $N$ は不変となり、 $||a||\rightarrow \alpha^2||a||$ となるので、$||a||=1$ とできる。
よってIV型である。
(iii) $\lambda_2=\pm1,\lambda_3=1$ のとき
このとき $||a||$ を規格化して $1$ にすることは常にできるわけではない。
なぜなら許される変換は以下のものであるためである。
許される変換は $a_2=a_3=0$ を保つ変換であるから、
$$
\begin{align}
T=\begin{pmatrix}
s & 0 \\
v & t
\end{pmatrix},
\ (s\in\mathbb{R},v\in\mathbb{R}^2,t\in GL(2,\mathbb{R}))
\end{align}
$$
の形であり、このとき、$N$ は
$$
\begin{align}
(\det T)T^{-1}N{}^tT^{-1}=s(\det t)
\begin{pmatrix}
0 & 0 \\
0 & t^{-1}n{}^tt^{-1}
\end{pmatrix},\ \
n={\rm diag}(\lambda_2,\lambda_3),
\end{align}
$$
と変換する。
この変換で $n$ が不変、すなわち $s(\det t)t^{-1}n{}^tt^{-1}=n$ であるためには、両辺の $\det$ を取って、$s/\det t=1$ となるから、$(\det t)^2t^{-1}n{}^tt^{-1}=n$ でなければならない。
またこの変換で $a\rightarrow sa$ と変換するから、$a_1\rightarrow (\det t)a_1$ と変換する。
(iii-a) $\lambda_2=\lambda_3=1$ のとき、$t\in O(2)$ である。
$\det t=\pm1$ であるから、$||a||=\beta$ の大きさを変えることはできない。
$\beta=0$ のときは $VII_0$ 型であるから、$\beta>0$ として $VII_\beta$ 型を得る。
(iii-b) $-\lambda_2=\lambda_3=1$ のとき、$t\in O(1,1)$ である。
$\det t=\pm1$ であるから、$||a||=\beta$ の大きさを変えることはできない。
$\beta=1$ のときは $III$ 型であるから、$\beta>0,\ \beta\ne1$ として $VI_\beta$ 型を得る。