Newton力学の舞台であるNewton時空を復習し、特殊相対性理論の舞台であるMinkowski時空を導入する。また基本的な概念や幾何学的性質を述べる。

Newton時空とMinkowski時空

特殊相対性理論の基本的概念とその性質を解説する。

特殊相対性理論

特殊相対論における力学を解説する。

特殊相対論的力学

特殊相対論における電磁気学を解説する。

電磁気学

　Newton力学においてある慣性系 $S$ の直交座標系を $\{t,x,y,z\}$ ($t$ は絶対時間) とする。
$S$ に対して、$x$ 方向に速度 $v$ で等速運動する慣性系 $X'$ の直交座標系を $\{t',x',y',z'\}$ とする。
$t=t'=0$ において、両者の原点が一致しているとすると、二つの座標系間の座標変換は
$$
\begin{align}
t&=t',\\
x&=x'+vt',\\
y&=y',\ z=z',
\end{align}
$$
で与えられる。これはGalilei変換と呼ばれる（ものの特別な場合である）。

　慣性系 $S$ における光速を $c$ とする。両系の原点が一致した瞬間に原点において光が全方向に発されたとする。このとき、慣性系 $S$ において光線の軌道 $(x(t),y(t),z(t))$ を考えると光速は $(dx/dt)^2+(dy/dt)^2+(dz/dt)^2=c^2$ であるから、$-(cdt)^2+dx^2+dy^2+dz^2=0$ を満たす。光速度不変の原理によれば、慣性系 $S'$ においても光線の軌道は $-(cdt')^2+dx'^2+dy'^2+dz'^2=0$ を満たさなければならない。しかし、上のGalilei変換は明らかにこれを満たさない。従って、特殊相対性理論においては互いに等速運動する慣性系間の座標変換としてGalilei変換を採用することはできない。

　ある慣性系において等速直線運動する粒子は別の慣性系でもそうであるべきという考察から、慣性系間の座標変換は線形変換と仮定する。線形変換でかつ $-(cdt)^2+dx^2+dy^2+dz^2=-(cdt')^2+dx'^2+dy'^2+dz'^2$ となる変換の成す群がPoincare群である。Galilei変換が３次元Euclid空間の等長変換となっていたことを参考にすると、Poincare群が等長変換となっている４次元時空、すなわちMinkowski時空を考え、慣性系間の座標変換をPoincare変換とする理論を建設すると都合が良さそうである。


Minkowski時空の導入の動機付け

ニュートン力学での時空概念を復習する。

**Newton時空(Newtonian spacetime)**とは、3次元ユークリッド空間 $\mathbb{E}$ と $\mathbb{R}$ の直積多様体 $\mathbb{R}\times \mathbb{E}$ のことである。
自然な射影を $T\colon\mathbb{R}\times E\rightarrow \mathbb{R},\ S\colon\mathbb{R}\times E\rightarrow E$ とする。
$T$ は**絶対Newton時間(Absolute Newtonian time)**と呼ばれる。

**世界線(World line)**とは、Newton時空の一次元部分多様体 $W$ で、$T|_W$ がある区間 $I\subset\mathbb{R}$ の上への微分同相写像となるようなもののことである。
粒子の軌道は世界線として理解される。
Newton時空の典型的な特徴は、全ての観測者に関して共通の時間、絶対Newton時間が定義されることである。


Newton時空

　Minkowski時空 $M$ において、**ベクトルポテンシャル** (vector potential) は１形式 $A$ として与えられる。
ベクトルポテンシャルはゲージ場の一種であるが、ここではゲージ理論については深入りしない。
さらに''電磁場'' (Electromagnetic field) は、２形式
$$
F=dA
$$
として定義される。

物理的に意味があるのは電磁場である。
任意の関数 $f\in C^\infty(M)$ に対して、ベクトルポテンシャルを 
$$
A'=A+df
$$
と変換しても、$F'=dA'=d(A+df)=dA=F$ となり、この変換で電磁場は不変である。
従って、このベクトルポテンシャルの変換は物理的な意味は持たない。
この変換は**ゲージ変換** (Gauge transformation) と呼ばれる。
これはゲージ理論における一般のゲージ変換のゲージ群を可換群にした特別な場合のものである。

観測者 $V\in T_pM$ に対して、$\{x^0,x^1,x^2,x^3\}$ を $\partial_0|_p=V$ となるLorentz座標を一つとる。
１形式 $E,B$ を
$$
\begin{align}
E&:=-c\partial_0\lrcorner F,\\
B&:=\partial_0\lrcorner(\ast F)
\end{align}
$$
と定義する。
ここで、$\lrcorner$ は内部積であり、体積要素は $dx^0\wedge dx^1\wedge dx^2\wedge dx^3=4!dx^{[1}\otimes dx^2\otimes dx^3\otimes dx^{4]}$ とする。
$E,B\in \Omega^1(M)$ を $V$ が観測する**電場** (Electric field)、**磁場** (Magnetic field)という。
$E,B$ の計量双対を取りベクトル場 ${}^\sharp E,{}^\sharp B\in \mathcal{X}(M)$ を電場、磁場と呼ぶこともあり、文脈に依存する。

電磁場 $F$ は Yang-Mills 方程式
$$
\delta F=\mu_0J
$$
を満たすことが要請される。
ここで $\delta$ は $d$ に対する余外微分、$J\in \Omega^1(M)$ は電流密度と呼ばれ物理的には電磁場を作り出す源となる。
また $J$ の係数は物理的な次元や符号を合わせるためのもので数学的には本質的ではない。
ただし、電流密度が0の領域でも電磁波のように非自明な解は存在する。
また電流密度を作り出す物質と電磁場も相互作用するので、実際には物質場の方程式と連立しなければならない。
しかしここでは、電流密度は外場とみなし（つまり、電磁場からの作用を受けない）、電磁場のみについて述べる。
特に、$J=0$ のときはこれらの事情を考える必要は普通ない。

一般的にはYang-Mills方程式はゲージ理論におけるゲージ場が従う方程式であり、先に述べたことは、電磁場の場合に制限したものであるが、形式的には同じである。
またYang-Mills方程式 $\delta F=J$ とBianchi恒等式 $dF=ddA=0$ を合わせて、Maxwell方程式と呼ぶ。


電磁場

　瞬間の観測者 $V\in T_pM$ に関して、任意の未来向き因果的ベクトル $X\in T_pM$ の時間-空間分解は
$$
\begin{aligned}
X=-g(V,X)V+\left(X+g(V,X)V\right)
\end{aligned}
$$
と表される。
ここで、
$$
\begin{aligned}
&-g(V,X)V\in\mathbb{R}V,\\
&X^{S(V)}\colon=X+g(V,X)V\in V^\perp
\end{aligned}
$$
である。

![時間-空間分解の概念図](/uploads/mathdown/OwBpJCrDNt3jKrKAhgUd.jpg =400)


因果的ベクトルの観測者に依存した時間-空間分解

　時空点 $p\in M$ を通過する世界線 $\alpha:I\ni\lambda\mapsto\alpha(\lambda)\in M,\ \alpha(0)=p$ を瞬間の観測者 $V\in T_pM$ が観測したときの $\alpha$ の速度を次のように定義する。

瞬間の観測者 $V\in T_pM$ と $p$ を通る因果的な世界線 $\alpha\colon I\rightarrow M,\ \alpha(0)=p,\ X=\frac{d\alpha}{d\lambda}(0)$ に対して、$V$ が時空点 $p$ において観測する $\alpha$ の空間的速度ベクトル $X^V$ を
$$
X^V\colon=-\frac{c}{g(V,X)}X^{S(V)}=-\frac{c}{g(V,X)}\left(X+g(V,X)V\right)
$$
とする。
$X^V$ は $X\to\alpha X$ という変換に対して不変である。

この定義の意味は次のようなものである。
すなわち、$X^{S(V)}$ は $V$ にとっての $\alpha$ の空間的な微小な移動距離（単位パラメータ $\lambda$ 当たり）であり、$-g(X,V)/c$ はその移動の間に経過した $V$ の固有時である。


瞬間の観測者の観測する速度

　ここではBianch恒等式とYang-Mills方程式を任意のLorentz座標 $\{x^0,x^1,x^2,x^3\}$ に関して具体的に書き下す。
ただし、時空は真空であるとする。
ギリシャ文字 $\mu,\nu,\lambda,\cdots$ は $0,1,2,3$ の値を取るとし、ラテン文字 $i,j,k,\cdots$ は $1,2,3$ の値を取るとする。

定義より、電場と磁場は $F_{i0}=E_i/c,\ F_{ij}=\sum_k\epsilon_{ijk}B_k$ である。
また３次元の空間的なベクトルを $\mathbb{E}=\sum_{k=1}^3E_k\partial_k,\ \mathbb{B}=\sum_{k=1}^3B_k\partial_k$ と定義する。

まず、Bianchi恒等式は、
$$
\begin{align}
dF=\frac{1}{3}\sum_{\mu,\nu,\lambda}(\partial_\mu F_{\nu\lambda}+\partial_\nu F_{\lambda\mu}+\partial_\lambda F_{\mu\nu})dx^\mu\wedge dx^\nu\wedge dx^\lambda=0
\end{align}
$$
であり、非自明なのは、(i) $\mu=0,1\le\nu=i,\lambda=j\le 3$、(ii) $1\le\mu=i,\nu=j,\lambda=k\le 3$ のときである。

(i) $\mu=0,1\le\nu=i,\lambda=j\le 3$ のとき

$$
\begin{align}
0&=\partial_0 F_{ij}+\partial_i F_{j0}+\partial_j F_{0i}\\
&=\epsilon_{ijk}\partial_0B_k+\frac{2}{c}\partial_{[i}E_{j]},\\
0&=2\partial_0B_k+\frac{2}{c}\epsilon_{kij}\partial_{[i}E_{j]},\\
0&=\partial_0B_k+\frac{1}{c}\epsilon_{kij}\partial_{i}E_{j},\\
&\partial_t\mathbb{B}+{\rm rot}\mathbb{E}=0
\end{align}
$$

(ii) $1\le\mu=i,\nu=j,\lambda=k\le 3$ かつ $i\ne j\ne k$ のとき

$$
\begin{align}
0&=\partial_i F_{jk}+\partial_j F_{ki}+\partial_k F_{ij},\\
0&=\sum_l(\epsilon_{jkl}\partial_i B_l+\epsilon_{kil}\partial_j B_l+\epsilon_{ijl}\partial_k B_l),\\
0&=\epsilon_{jki}\partial_i B_i+\epsilon_{kij}\partial_j B_j+\epsilon_{ijk}\partial_k B_k,\\
&{\rm div}\mathbb{B}=0
\end{align}
$$

次にYang-Mills方程式を書き下す。
$$
\begin{align}
\delta F&=-\partial^\mu F_{\mu\nu}dx^\nu,\\
&=-\frac{1}{c}\partial_iE_idx^0+\left(-\frac{1}{c}\partial_0E_i-\partial_jF_{ji}\right)dx^i,\\
&=-\frac{1}{c}\partial_iE_idx^0+\left(-\frac{1}{c}\partial_0E_i+\epsilon_{ijk}\partial_jB_k\right)dx^i,\\
&=-\frac{1}{c}{\rm div}\mathbb{E}dx^0+\left(-\frac{1}{c^2}\partial_tE_i+({\rm rot}\mathbb{B})_i\right)dx^i
\end{align}
$$
である。
さらに、４元電流密度を
$$
\begin{align}
J:=c\rho\partial_0+\sum_{k=1}^3j_k\partial_k
\end{align}
$$
と定義する。
よって、$\delta F=\mu_0J$ より、
$$
\begin{align}
&{\rm div}\mathbb{E}=\frac{\rho}{\varepsilon_0},\\
&{\rm rot}\mathbb{B}-\frac{1}{c^2}\partial_t\mathbb{E}=\mu_0\mathbb{j}
\end{align}
$$
を得る。

以上に現れた４つの式
$$
\begin{align}
&\partial_t\mathbb{B}+{\rm rot}\mathbb{E}=0,\\
&{\rm div}\mathbb{B}=0,\\
&{\rm div}\mathbb{E}=\frac{\rho}{\varepsilon_0},\\
&{\rm rot}\mathbb{B}-\frac{1}{c^2}\partial_t\mathbb{E}=\mu_0\mathbb{j}
\end{align}
$$
はMaxwell方程式と呼ばれる。
従って、Maxwell電磁気学は任意の慣性的観測者に対して成り立つ。


Maxwell方程式

特殊相対性理論の舞台となるのはNewton時空ではなく、Minkowski時空である。Minkowski時空の基本的な幾何学的性質や定義を述べる。


&&&def Minkowski時空
微分多様体 $\mathbb{R}^{4}$ の標準的な直交座標 $\{x^0,x^1,x^2,x^3\}$ に関して、
$$
\begin{aligned}
g=-(dx^0)^2+(dx^1)^2+(dx^2)^2+(dx^3)^2
\end{aligned}
$$
で与えられる擬リーマン計量を備えた擬リーマン多様体 $(\mathbb{R}^4,g)$ を $\mathbb{E}^{(1,3)}$ と表す。**Minkowski時空(Minkowski spacetime)**とは $\mathbb{E}^{(1,3)}$ と等長同型なローレンツ多様体 $M$ のことである。あるいは単連結完備平坦Lorentz多様体と定義してもよい。以下特に断らない限り $M$ でMinkowski時空を表す。
&&&

Minkowski時空の物理において重要なのが次の慣性座標系である。

&&&def 
Minkowski時空 $M$ の**Lorentz座標**または**慣性座標(inertial coordinate)**とは、等長写像 $\varphi:M\rightarrow \mathbb{E}^{(1,3)}(\simeq\mathbb{R}^4)$ のことである。
&&&

Newton時空でも慣性座標という言葉は使うことがあるので、ここでは誤解を避けるためLorentz座標という言葉を使う。

$\mathbb{E}^{(1,3)}$ の等長変換群は**Poincare群**と呼ばれる。$\mathbb{E}^{(1,3)}$ の正規直交座標系 $\{x^0,x^1,x^2,x^3\}$ を一つ任意に固定すると、Poincare群の元は $x^i\mapsto \Lambda^i_{\ j}x^j+a^i$ と表される。
ここで、$\Lambda=(\Lambda^i_{\ j})$ は $O(1,3):=\{\Lambda\in GL(4,\mathbb{R});\ {}^t\Lambda\mathbb{I}_{(1,3)}\Lambda=\mathbb{I}_{(1,3)}\}$ の元であり、$a={}^t(a^0,a^1,a^2,a^3)\in\mathbb{R}^4$ である。
ただし、
$$
\begin{align}
\mathbb{I}_{(1,3)}=\begin{pmatrix}
-1 & 0 & 0 & 0 \\
0  & 1 & 0 & 0 \\
0  & 0 & 1 & 0 \\
0  & 0 & 0 & 1 \\
\end{pmatrix}
\end{align}
$$
である。$O(1,3)$ は**Lorentz群**と呼ばれる。２つのLorentz座標系 $\varphi_i:M\rightarrow\mathbb{E}^{(1,3)},\ (i=1,2)$ に対して、この２つの座標系の間の座標変換 $\varphi_1^{-1}\circ\varphi_2$ は、明らかに $\mathbb{E}^{(1,3)}$ の等長変換である。

Minkowski時空の接ベクトルにはその因果的特性に応じて以下の名前がある。

&&&def 
Minkowski時空の接ベクトル $X$ は $||X||^2<0$ のとき**時間的(timelike)**、$||X||^2>0$ のとき**空間的(spacelike)**、$||X||^2=0$ のとき**光的(null,lightlike)**という。また空間的でないものを**因果的(causal, non-spacelike)**という。またLorentz座標 $\varphi$を一つ固定するとき、因果的な接ベクトル $X$ は、$-g(X,\partial_0)>0$ のとき**未来向き(future-directed)**といい、$-g(X,\partial_0)<0$ のとき**過去向き(past-directed)**であるという。
&&&

Lorentz座標 $\varphi$ は $M$ の接ベクトルに時間的向きを定義する。これを$\varphi$が誘導時間的向きと呼ぶ。以降は $M$ の時間的向きを一つ固定して議論する。

粒子の世界線は次のように定義される。

&&&def 
有質量粒子(massive particle)の世界線とは、timelikeな未来向きの区分的滑らかな曲線のことである。

無質量粒子(massless particle)の世界線とは、未来向きの区分的滑らかな光的測地線のことである。
&&&

慣性系の存在に関する基本的な性質は以下である。

&&&lem 
任意の $p\in M$ と $T_pM$の任意の正規直交基底 $\{e_i\}$ に対して、Lorentz座標 $\{x^0,x^1,x^2,x^3\}$ で $\partial_i|_p=e_i,\ (0\le i\le 3)$ となるものがただ一つ存在する。
&&&

&&&prf 
$\{e_i\}$ が定義する正規座標 $\xi$ は求める性質を持つ。同じ性質を持つLorentz座標 $\eta$ があれば、$\xi\circ\eta^{-1}$ は $\mathbb{R}^{(1,3)}$ の等長変換で、かつある正規直交基底を固定する。従って、$\xi=\eta$ である。
&&&


Minkowski時空

# 原理
特殊相対性理論は力学と電磁気現象に関する理論であり、さらに重力をも扱えるのが一般相対性理論であるが、それらを建設する上で次の二つの事が基本的な指針となっている。これらは特殊でも一般でも関係なく要請されるべきものである。

（I）相対性原理：物理法則は時空をローレンツ多様体と見なして、その幾何学構造、特に計量テンソル場によって定式化されるべきである。

(II)光速不変の原理：真空において、光速は光源と観測者の相対運動によらずいかなる観測者が観測しても $c\sim299,792km/s$である。

# 基本的な概念

## 観測者、瞬間の観測者
有質量粒子の世界線
$$
\alpha\colon \mathbb{R}\supset I\ni \lambda\mapsto \alpha(\lambda)\in M
$$
で $\left|\left|\frac{d\alpha}{d\lambda}\right|\right|^2=-1$ となるものを**観測者** (Observer)という。さらに時空点 $p\in M$ における**瞬間の観測者** (instantaneous observer) とは、$V\in T_pM$ で $||V||^2=-1$ となるもののことをいう。瞬間の観測者は時空点 $p$ において瞬間的に等速直線運動している観測者を表現している。また**慣性的観測者** (inertial observer) とは 弧長でパラメータ付けされた未来向きの時間的測地線のことである。慣性的観測者のことを**慣性系**（inertial system）とも呼ぶ。

瞬間の観測者 $V\in T_pM$ に対して、Lorentz座標系 $\{x^0,x^1,x^2,x^3\}$ で $\partial_0|_p=V$ となるものを $V$ に関する**慣性座標系**または単に**慣性系**と呼ぶことにする。$V$ に関する慣性座標系は一意的ではない。

瞬間の観測者 $V\in T_pM$ に対して、ある慣性的観測者 $\mathbb{R}\ni t\mapsto c(t)\in M$ で $c(0)=p,\ \dot{c}(0)=V$ となるものが存在する。文脈に応じてこの２つはしばしば同一視して議論される。

２つの慣性系は定義より $M$ の等長変換群であるPoincare群の作用により写りあう。以下では、慣性系に対する観測可能な物理量や物理法則を与えるが、これらは相対性原理の要請により、等長変換により不変である。また慣性系が観測する速度を定義した後で、２つの慣性系は互いに等速運動の関係にあることが分かる。従って、互いに等速運動する慣性的観測者が観測する物理法則は完全に一致するため、物理的に区別することはできない。これを**特殊相対性原理** (Principle of special relativity)という。


## 固有時
任意の有質量粒子の世界線 $\alpha:I\rightarrow M$ に対して、この曲線の長さを
$$
s=\int_a^b\sqrt{-\left|\left|\frac{d\alpha}{d\lambda}\right|\right|^2}d\lambda
$$
とするとき、
$$
\tau=\frac{s}{c}
$$
をこの世界線の**固有時** (proper time)という。ここで積分区間 $[a,b]\subset I$ は任意に選ぶ。このとき、事象 $\alpha(a)$ と $\alpha(b)$の間にこの世界線に沿う観測者が経験する時間が $\tau$ であると定義する。

無質量粒子の世界線は未来向きの区分的滑らかな光的測地線であるから固有時は常に0である。光的測地線のアフィンパラメータは固有時とは呼ばない。

## 観測者に依存した時刻一定面
Newton力学では全ての観測者にとって時間は同等に経過すると仮定している。一方、Minkowski時空の力学では、時刻一定面を観測者に依存して次のように定義する。すなわち、瞬間の観測者 $V\in T_pM$ に対して、$T_pM$ の正規直交基底 $\{e_0=V,e_1,e_2,e_3\}$ を任意に一つ取る。このとき、Lorentz座標 $\{x^0,x^1,x^2,x^3\}$ が存在して $\partial_i|_p=e_i,\ (0\le i\le3)$ となる。このとき、$x^0=x^0(p)$の集合は $M$ の超曲面（超平面）であり、これを観測者 $V$ のこの瞬間の時刻一定面と定義する。さらに、$T_pM$ は $T_pM=\mathbb{R}V\oplus V^\perp$ と直交分解される。ここで $V^\perp$ は $V$ に直交する部分空間である。この分解を観測者 $V$ に関する**時間-空間分解**または **$1+3$ 分解**という。また、${\rm exp}_p(V^\perp)=\{(x^0,x^1,x^2,x^3)\in M;\ x^0=x^0(p) \}$ であるから、$V^\perp$ と $V$ の時刻一定面はしばしば同一視される。

![観測者 $V,W$ に関する時間-空間分解](/uploads/mathdown/DiLBuk7OSMIZqEHGM5Ml.jpg =300)

このことから、時刻一定面は観測者に依存する。従って、ある観測者にとって同時に起きている２つの事象が別の観測者にとっては時間的な関係になっていることがあり得る。同時刻の事象の集合が観測者に依存して決定されることを**同時刻の相対性**と呼ぶ。時刻一定面の観測者への依存性こそ特殊相対論のNewton力学とは異なった様々な性質を導く要因となっている。



特殊相対性理論の原理と基本的な概念

　真空中の電磁場 $F$ に対して、''エネルギー運動量テンソル''を
$$
\begin{align}
T(X,Y)=\frac{1}{\mu_0}\left(g^\ast(X\lrcorner F,Y\lrcorner F)-\frac{1}{4}||F||^2g(X,Y)\right)
\end{align}
$$
と定義する。
ここで、$g^\ast$ は双対接空間に定義される内積である。
チャートに関して成分表示すると
$$
\begin{align}
T_{\mu\nu}=\frac{1}{\mu_0}\left(F_{\mu\rho}F_\nu^{\ \rho}-\frac{1}{4}F_{\rho\omega}F^{\rho\omega}g_{\mu\nu}\right)
\end{align}
$$
である。


&&&prop 
あるLorentz座標系 $\{x^0,x^1,x^2,x^3\}$ に関して、
$$
F=\sum_i\frac{1}{c}E_idx^i\wedge dx^0+\frac{1}{2}\sum_{i,j,k}\epsilon_{ijk}B_idx^j\wedge dx^k
$$
と表すとき、
$$
\begin{align}
T_{00}&=\frac{1}{2}(\mathbb{E}\cdot\mathbb{D}+\mathbb{H}\cdot\mathbb{B}),\\
T_{i0}&=-\frac{1}{c}\mathbb{S}_i,\ \mathbb{S}=\mathbb{E}\times\mathbb{H},\\
T_{ij}&=-\epsilon_0E_iE_j-\mu_0H_iH_j+\frac{1}{2}(\mathbb{E}\cdot\mathbb{D}+\mathbb{H}\cdot\mathbb{B})\delta_{ij}
\end{align}
$$
となる。
ただし、$\mathbb{D}=\varepsilon_0\mathbb{E},\mathbb{B}=\mu_0\mathbb{H}$ である。
&&&

&&&prf 
\begin{align}
||F||^2&=2(\sum_iF_{0i}F^{0i}+\sum_{i<j}F_{ij}F^{ij})=-\frac{2}{c^2}|\mathbb{E}|^2+2|\mathbb{B}|^2,\\
T_{00}&=\frac{1}{\mu_0}(F_0^{\ \alpha}+F_{0\alpha}+\frac{1}{4}||F||^2)
=\frac{1}{\mu_0}(\frac{1}{c^2}|\mathbb{E}|^2-\frac{1}{2c^2}|\mathbb{E}|^2+\frac{1}{2}|\mathbb{B}|^2)
=\frac{1}{2}(\mathbb{E}\cdot\mathbb{D}+\mathbb{H}\cdot\mathbb{B}),\\
T_{i0}&=\frac{1}{\mu_0}F_0^{\ \nu}F_{i\nu}=-\frac{1}{\mu_0}F_{j0}F_i^{\ j}=-\frac{1}{\mu_0c}\sum_{j,k}E_j\epsilon_{ijk}B_k
=-\frac{1}{c}(\mathbb{E}\times\mathbb{H})_i,\\
T_{ij}&=\frac{1}{\mu_0}(F_i^{\ \mu}F_{j\mu}-\frac{1}{4}F_{\mu\nu}F^{\mu\nu}g_{ij})
=\frac{1}{\mu_0}(F_i^{\ 0}F_{j0}+F_{ik}F_{jk}+\frac{1}{2}(|\mathbb{E}|^2/c^2-|\mathbb{B}|^2)\delta_{ij})\\
&=\frac{1}{\mu_0}(-\frac{1}{c^2}E_iE_j+\epsilon_{ikl}\epsilon_{jkm}B_lB_m+\frac{1}{2}(|\mathbb{E}|^2/c^2-|\mathbb{B}|^2)\delta_{ij})\\
&=-\varepsilon_0E_iE_j+\frac{1}{\mu_0}(\delta^i_j\delta^l_m-\delta^i_m\delta^l_j)B_lB_m+\frac{1}{2}(\mathbb{E}\cdot\mathbb{D}-\mathbb{B}\cdot\mathbb{H})\delta_{ij},\\
&=-\varepsilon_0E_iE_j+\mathbb{B}\cdot\mathbb{H}\delta_{ij}-\frac{1}{\mu_0}B_jB_i+\frac{1}{2}(\mathbb{E}\cdot\mathbb{D}-\mathbb{B}\cdot\mathbb{H})\delta_{ij}
=-\varepsilon_0E_iE_j-\mu_0H_iH_j+\frac{1}{2}(\mathbb{E}\cdot\mathbb{D}+\mathbb{B}\cdot\mathbb{H})\delta_{ij}
\end{align}
&&&

さらに、次が成り立つ。

&&&prop 

$$
\begin{align}
\partial^\mu T_{\mu\nu}=\mu_0F_\nu^{\ \mu}J_\mu
\end{align}
$$
&&&

&&&prf 
\begin{align}
\partial^\mu T_{\mu\nu}&=\partial^\mu(F_{\mu\lambda}F_\nu^{\ \lambda}-\frac{1}{4}F_{\lambda\rho}F^{\lambda\rho}g_{\mu\nu}),\\
&=\partial^\mu F_{\mu\lambda}F_\nu^{\ \lambda}+F_{\mu\lambda}\partial^\mu F_\nu^{\ \lambda}-\frac{1}{4}\partial^\mu(F_{\lambda\rho}F^{\lambda\rho})g_{\mu\nu},\\
&=\partial^\mu F_{\mu \lambda}F_\nu^{\ \lambda}+F_{\mu \lambda}\partial^\mu F_\nu^{\ \lambda}-\frac{1}{2}(\partial_\nu F_{\lambda\rho})F^{\lambda\rho},\\
&=\partial^\mu F_{\mu\lambda}F_\nu^{\ \lambda}+F_{\mu\lambda}\partial^\mu F_\nu^{\ \lambda}+\frac{1}{2}(\partial_\lambda F_{\rho\nu}+\partial_\rho F_{\nu\lambda})F^{\lambda\rho},\\
&=\partial^\mu F_{\mu \lambda}F_\nu^{\ \lambda}=\mu_0F_\nu^{\ \lambda}J_\lambda,\ (\because\ \partial^\mu F_{\mu\nu}=\mu_0J_\nu)
\end{align}
&&&


また、上の式を時間と空間の成分に分解すると次が得られる。

&&&prop 
\begin{align}
-\frac{\partial w}{\partial t}&={\rm div}\mathbb{S}+\mathbb{E}\cdot\mathbb{j},\\
\frac{1}{c^2}\frac{\partial\mathbb{S}}{\partial t}&={\rm div}\mathbb{M}-(\rho\mathbb{E}+\mathbb{j}\times\mathbb{B})
\end{align}
となる。ただし、
\begin{align}
J&=\rho dx^0-\sum_{k=1}^3j_kdx^k,\\
w&:=\frac{1}{2}(\mathbb{E}\cdot\mathbb{D}+\mathbb{H}\cdot\mathbb{B}),\\
M_{ij}&:=-T_{ij}=\epsilon_0E_iE_j+\mu_0H_iH_j-\frac{1}{2}(\mathbb{E}\cdot\mathbb{D}+\mathbb{H}\cdot\mathbb{B})\delta_{ij},\\
{\rm div}\mathbb{M}&=\sum_{i,j=1}^3\partial_iM_{ij}\partial_j
\end{align}
と置いた。
&&&

&&&prf 
\begin{align}
\partial^\mu T_{\mu0}
&=\partial^0T_{00}+\partial^iT_{i0}
=-\frac{1}{c}\frac{\partial w}{\partial t}-\frac{1}{c}\partial_iS_i
\\
\mu_0F_0^{\ \mu}J_\mu
&=\mu_0F_{0\mu}J^\mu
=\mu_0F_{0i}J^i
=-\mu_0\frac{1}{c}E_iJ^i
=\mu_0\frac{1}{c}E_ij^i,\\
\partial^\mu T_{\mu i}
&=\partial^0T_{0i}+\partial^jT_{ji}
=\frac{1}{c^2}\partial_tS_i-\partial^jM_{ji},
\\
\mu_0F_i^{\ \mu}J_\mu
&=\mu_0F_{i0}J^0+\mu_0F_{ij}J^j
\end{align}
&&&



電磁場のエネルギー運動量テンソル

　瞬間の観測者 $V\in T_pM$ と 任意の因果的ベクトル $X\in T_pM$ に対して、
$$
||X^V||^2=\frac{c^2||X||^2}{g(X,V)^2}+c^2\le c^2
$$
となる。
これは任意の因果的世界線を任意の観測者が観測してもその空間的速さが光速 $c$ を超えないことを意味している。
さらに $X$ が光的であるときは、$||X^V||^2=c^2$ である。
これは実際の実験結果である光速不変の原理を表現している。

Lorentz座標 $\{x^0,x^1,x^2,x^3\}$ を適当に取れば、時空点 $p\in M$ における瞬間の観測者は $V=(\partial_0)_p$ と表される。
このとき、$X=\cosh\theta\partial_0+\sinh\theta\partial_1$ としてよい。
よって、$X^V=c\tanh\theta\partial_x$ を得る。
このことから、$V$ が観測する $X$ の $x$ 方向の速度（符号付き）を $v$ とすると、$\tanh\theta=\frac{v}{c}$ である。
$V$ と $X$ の時空でのなす角 $\theta$ が大きいほど、速さは光速 $c$ に近づく。

このように特殊相対性理論とNewton力学との顕著な違いの一つは物理的に意味のある最高速度は光速であり、その世界線は光的測地線となることである。
従って、空間的に離れた時空の任意の２点は因果的に関係することはできない。
Newton力学ではそれが可能な場合もある。


速度限界と光速不変の原理

　３つの瞬間の観測者 $X,Y,Z\in T_pM$ が一次従属であるとする。
$T_pM$ の基底 $\{\partial_0,\partial_1,\partial_2,\partial_3\}$ を適当に取り、$X=\partial_0,\ Y=\cosh\theta\partial_0+\sinh\theta\partial_1,\ Z=\cosh\phi\partial_0+\sinh\phi\partial_1,\ 0\le\theta\le\phi$ としてよい。
このとき、$v_1=|Y^X|=c\tanh\theta,\ v_2=|Z^Y|=c\tanh(\phi-\theta)$ であるから、
$$
\begin{aligned}
v=|Z^X|=\tanh\phi=\tanh(\phi-\theta+\theta)=\frac{v_1/c+v_2/c}{1+v_1v_2/c^2}
\end{aligned}
$$
となる。


速度合成

　２つの慣性系間の座標変換はLorentz変換であるから、それぞれの座標系に関する電磁場 $F$ の成分も2形式の変換規則に従い変換される。具体的には、二つの慣性系 $S,S'$ があり、$S$ のLorentz座標系を $\{x^\mu\}$、$S'$ のLorentz座標系を $\{y^\mu\}$ とする。慣性系 $S$ において、電磁場が
$$
\begin{align}
F&=F_{\mu\nu}dx^\mu\wedge dx^\nu,\\
&=\frac{E_i}{c}dx^i\wedge dx^0+\sum_{i<j}\sum_k\epsilon_{ijk}B_kdx^i\wedge dx^j
\end{align}
$$
と表されたとすると、慣性系 $S'$ においては、
$$
\begin{align}
F=F_{\mu\nu}\frac{\partial x^\mu}{\partial y^\alpha}\frac{\partial x^\nu}{\partial y^\beta}dy^\alpha\wedge dy^\beta
\end{align}
$$
となる。
従って電場、磁場という概念は慣性系に依存した概念であることがわかる。
より明示的な表示を得るために、$S'$ 系が $S$ 系の $x^1$ 軸の方向へ速さ $v$ で等速に移動している状況、すなわち
$$
\begin{align}
x^0&=\cosh\theta y^0+\sinh\theta y^1,\\
x^1&=\sinh\theta y^0+\cosh\theta y^1,\\
x^2&=y^2,\\
x^3&=y^3,\\
\tanh\theta&=v/c
\end{align}
$$
が成り立っているとする。
このとき、
$$
\begin{align}
F&=\frac{E_1}{c}dx^1\wedge dx^0+\frac{E_2}{c}dx^2\wedge dx^0+\frac{E_3}{c}dx^3\wedge dx^0+B_3dx^1\wedge dx^2+B_2dx^3\wedge dx^1+B_1dx^2\wedge dx^3,\\
&=\frac{E_1}{c}(\sinh\theta dy^0+\cosh\theta dy^1)\wedge(\cosh\theta dy^0+\sinh\theta dy^1)
+\frac{E_2}{c}dy^2\wedge (\cosh\theta dy^0+\sinh\theta dy^1)\\
&+\frac{E_3}{c}dy^3\wedge (\cosh\theta dy^0+\sinh\theta dy^1)
+B_3(\sinh\theta dy^0+\cosh\theta dy^1)\wedge dy^2
+B_2dy^3\wedge (\sinh\theta dy^0+\cosh\theta dy^1)\\
&+B_1dy^2\wedge dy^3,\\
&=\frac{E_1}{c}dy^1\wedge dy^0
+(\frac{E_2}{c}\cosh\theta-B_3\sinh\theta) dy^2\wedge dy^0
+(\frac{E_3}{c}\cosh\theta+B_2\sinh\theta) dy^3\wedge dy^0\\
&+(-\frac{E_2}{c}\sinh\theta+B_3\cosh\theta) dy^1\wedge dy^2
+(\frac{E_3}{c}\sinh\theta+B_2\cosh\theta) dy^3\wedge dy^1
+B_1dy^2\wedge dy^3
\end{align}
$$
となる。
よって
$$
\begin{align}
E'_1&=E_1,\\
E'_2&=E_2\cosh\theta-cB_3\sinh\theta=\frac{E_2-B_3v}{\sqrt{1-(v/c)^2}},\\
E'_3&=E_3\cosh\theta+cB_2\sinh\theta=\frac{E_3+B_2v}{\sqrt{1-(v/c)^2}},\\
B'_1&=B_1,\\
B'_2&=\frac{E_3}{c}\sinh\theta+B_2\cosh\theta=\frac{B_2+E_3v/c^2}{\sqrt{1-(v/c)^2}},\\
B'_3&=-\frac{E_2}{c}\sinh\theta+B_3\cosh\theta=\frac{B_3-E_2v/c^2}{\sqrt{1-(v/c)^2}}
\end{align}
$$
と変換することが分かる。
従って、$S$ 系から見た $S'$ 系の運動方向を $\mathbb{v}$ とすると(この方向を $x^1$ 方向に取ることは常にできるから)、
$$
\begin{align}
\mathbb{E}'_{||}&=\mathbb{E}_{||},\\
\mathbb{E}'_{\perp}&=\frac{\mathbb{E}_{\perp}+\mathbb{v}\times\mathbb{B}}{\sqrt{1-(v/c)^2}},\\
\mathbb{B}'_{||}&=\mathbb{B}_{||},\\
\mathbb{B}'_{\perp}&=\frac{\mathbb{E}_{\perp}-\mathbb{v}\times\mathbb{E}/c^2}{\sqrt{1-(v/c)^2}},
\end{align}
$$
となる。
ここで、$||,\perp$ はそれぞれ $\mathbb{v}$ に平行な成分と垂直な成分を表す。

具体例として点電荷が静止している系と等速運動している系での電場、磁場の関係を計算する。
$S'$ 系の原点に電荷 $e$ の点電荷が静止していて、この電荷が作り出す電磁場が
$$
\begin{align}
F&=\frac{E'_i}{c}dy^i\wedge dy^0,\\
E'_i(y)&=\frac{e}{4\pi\epsilon_0}\frac{y^i}{r'^3},\\
r'&=\sqrt{(y^1)^2+(y^2)^2+(y^3)^2}
\end{align}
$$
であるとする。
これはCoulombの法則により発生する電場である。
このとき、上の変換式で $\mathbb{E},\mathbb{B}$ の'ありなしを入れ替えて、$\mathbb{v}$ を $-\mathbb{v}$ にすると、
$$
\begin{align}
\mathbb{E}&=\frac{e}{4\pi\epsilon_0}\frac{\mathbb{x}-\mathbb{v}t}{((x^1-vt)^2+(x^2)^2+(x^3)^2)^{3/2}\sqrt{1-(v/c)^2}},\\
\mathbb{B}&=\frac{1}{c^2}\mathbb{v}\times\mathbb{E}
\end{align}
$$
となる。
第二式は $v=|\mathbb{v}|$ が小さいときは、近似的に電流が作り出す磁場の公式であるBiot-Savartの法則を与える。


慣性系による電磁場の現れ方の違い

　ある観測者に対して物体が運動しているとする。
このとき、その観測者の測定するその物体の運動方向への空間的長さは、その物体の静止系で測定される長さに比べて小さいということが結論される。
これを**ローレンツ収縮** (Lorentz contraction)と呼ぶ。

この現象はMinkowski時空の幾何学として以下のように理解される。
ある観測者 $V\in T_pM$ が $p=(0,0,0,0),\ V=\partial_0$ と表されるようなLorentz座標 $\{x^0,x^1,x^2,x^3\}$ を一つ固定する。
観測者 $V$ のこの瞬間（時空点 $p$）の時間一定面は $\{(0,x^1,x^2,x^3)\in M\}$ である。
一方、$V$ から見て $\partial_1$ 方向へ速さ $v$ で移動する観測者 $V_\theta\in T_pM,\ \tanh\theta=v/c$ のこの瞬間の時間一定面は、
$$
\begin{aligned}
&\{(\sinh\theta x^1,\cosh\theta x^1,x^2,x^3)\in M\},\\
&\sinh\theta=\frac{v/c}{\sqrt{1-(v/c)^2}},\ \cosh\theta=\frac{1}{\sqrt{1-(v/c)^2}}
\end{aligned}
$$
である。

このとき、ある観測者がある時刻に見た物体の空間的な大きさは、その観測者の時刻一定面とその物体がはく時空領域（物体の４次元的領域）の共通部分のことと定義する。

従って、物体の長さも観測者に依存する。
いま、２つの粒子の世界線がそれぞれ $c_1(t)=(ct,0,0,0),\ c_2(t)=(ct,L,0,0)$ であるとする。
ここで $t$ は $V$ の固有時である。
観測者 $V$ から見たこの２つの粒子の空間的な距離は $L$ である。
一方、$V_\theta$ の時刻一定面 $\Pi_\theta$ 上を $p$ から $x^1$ 方向へ距離 $\lambda$ 進んだ点は $(\sinh\theta,\cosh\theta,0,0)\lambda$ であるから、$\Pi_\theta$ と $c_2(t)$ の共有点は、
$$
\begin{aligned}
(\sinh\theta,\cosh\theta,0,0)\lambda=(ct,L,0,0),\\
\therefore\ \lambda=\frac{L}{\cosh\theta}
\end{aligned}
$$
で与えられる。
従って、この瞬間、観測者 $V_\theta$ にとっての $c_1,c_2$ の空間的距離 $L'$ は、
$$
\begin{aligned}
L'=L\sqrt{1-(v/c)^2}\ (<L)
\end{aligned}
$$
である。
このように、相対運動する方向に広がった物体は縮んで見える。

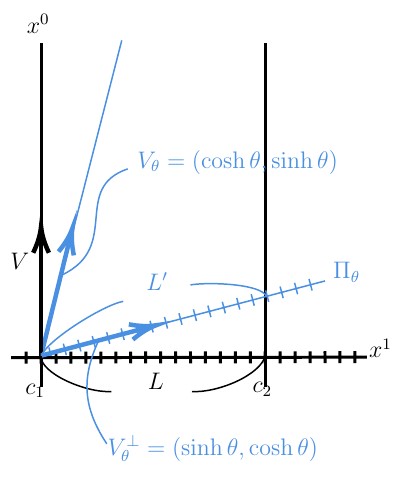![Lorentz収縮の概念図](/uploads/mathdown/uKMDvgh8B1CV3HibyaAY.jpg =400)


ローレンツ収縮

　互いに運動する観測者は自分の固有時と相手の固有時の差異を観測することを解説する。

最も単純な状況として互いに等速直線運動する２つの観測者を考えよう。
あるLorentz座標において、ある観測者が $c_1(\tau_1)=(c,0,0,0)\tau_1$ と表されているとする。
また $c_1$ に対して、$x^1$ 方向へ速度 $v$ で等速直線運動する観測者を $c_2(\tau_2)=(\cosh\theta,\sinh\theta,0,0)c\tau_2,\ (\tanh\theta=v/c)$ とする。
このとき、$c_1,c_2$ の共有点をそれぞれの固有時0の点とし、それぞれの固有時を $\tau_1,\tau_2$ とする。
すると、$c_2$ の固有時 $\tau_2=1$ の事象、すなわち $c_2(1)$ は観測者 $c_1$ にとっては固有時 $\tau_1=\cosh\theta$ の時刻一定面、すなわち $\{(\cosh\theta,x^1,x^2,x^3)\in M\}$ 上の事象である。
このことから、例えば、$c_1$ が $c_2$ と共に運動する時計を観測したとき、$c_1$ の時計で $\cosh\theta$ 秒かけて $c_1$ の時計が1秒を刻むのを観測することになり、$c_1$ は $c_2$ の時計が自分より遅れているように見える。

またこの議論で $c_1,c_2$ の役割を入れ替えることもできるので、$c_2$ も $c_1$ の時計が自分より遅れているように見えることが分かる。
このことから、互いに等速度で相対運動する観測者は互いに相手の時計の進みが遅れていることを観測する。

![経過時間の相対性の概念図](/uploads/mathdown/WlBzcLv8euWyH3jyewaY.jpg =400)


経過時間の相対性

　質量 $m$ の粒子の固有時パラメータ付けされた世界線を $\gamma:I\in \tau\mapsto\gamma(t)\in M$ とする。
このとき
$$
p=m\frac{d\gamma}{d\tau}
$$
をこの粒子 $\gamma$ の**4元運動量**(4-momentum)と呼ぶ。
点 $\gamma(\tau)$ における観測者を $V\in T_{\gamma(\tau)}M$ とするとき、$V$ が観測する $\gamma$ の運動量を
$$
p^{S(V)}=p+g(p,V)V\ \in T_{\gamma(\tau)}M
$$
と定義する。
さらに $V$ が観測する $\gamma$ のエネルギー $E_\gamma^V$ を
$$
E_\gamma^V:=-c\ g(p,V)
$$
と定義する。

適当なLorentz座標 $\{x^0,x^1,x^2,x^3\}$ を取ると、$V=\partial_0$、$X\colon=\frac{d\gamma}{d\tau}=c\cosh\theta\partial_0+c\sinh\theta\partial_1,\ (\tanh\theta=v/c)$ と表される。
このとき、$V$ が観測する $\gamma$ のエネルギーは
\begin{align}
E^V_\gamma=-cmg(X,V)=mc^2\cosh\theta&=\frac{mc^2}{\sqrt{1-(v/c)^2}}\\
&=mc^2+\frac{1}{2}mv^2+\cdots
\end{align}
となる。

$v=0$ のとき、
$$
E_\gamma^V=mc^2
$$
となる。
これは**Einsteinの公式**と呼ばれ、たぶん特殊相対論において一番有名な式である。


エネルギー、運動量

特殊相対性理論は重力を含まない電磁力学の理論としてEinsteinにより提唱され、現代ではMinkowski時空の幾何学として定式化される。