経過時間の相対性
互いに運動する観測者は自分の固有時と相手の固有時の差異を観測することを解説する。
最も単純な状況として互いに等速直線運動する2つの観測者を考えよう。
あるLorentz座標において、ある観測者が $c_1(\tau_1)=(c,0,0,0)\tau_1$ と表されているとする。
また $c_1$ に対して、$x^1$ 方向へ速度 $v$ で等速直線運動する観測者を $c_2(\tau_2)=(\cosh\theta,\sinh\theta,0,0)c\tau_2,\ (\tanh\theta=v/c)$ とする。
このとき、$c_1,c_2$ の共有点をそれぞれの固有時0の点とし、それぞれの固有時を $\tau_1,\tau_2$ とする。
すると、$c_2$ の固有時 $\tau_2=1$ の事象、すなわち $c_2(1)$ は観測者 $c_1$ にとっては固有時 $\tau_1=\cosh\theta$ の時刻一定面、すなわち $\{(\cosh\theta,x^1,x^2,x^3)\in M\}$ 上の事象である。
このことから、例えば、$c_1$ が $c_2$ と共に運動する時計を観測したとき、$c_1$ の時計で $\cosh\theta$ 秒かけて $c_1$ の時計が1秒を刻むのを観測することになり、$c_1$ は $c_2$ の時計が自分より遅れているように見える。
またこの議論で $c_1,c_2$ の役割を入れ替えることもできるので、$c_2$ も $c_1$ の時計が自分より遅れているように見えることが分かる。
このことから、互いに等速度で相対運動する観測者は互いに相手の時計の進みが遅れていることを観測する。
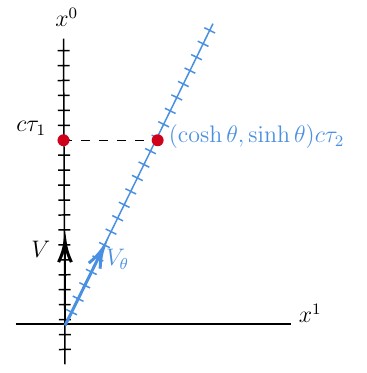 経過時間の相対性の概念図
経過時間の相対性の概念図
