Chronological時空
Totally Viciousでない時空をNon-Totally Vicious時空と呼ぶ。定義よりNon-T.V.時空にはCTCが存在している可能性がまだある。CTCは因果構造的には好ましくないためCTCが全く存在していないクラスの時空を定義することは自然である。
区分的 $C^1$ 級CTCが存在しない時空をchronological(順時)時空という。
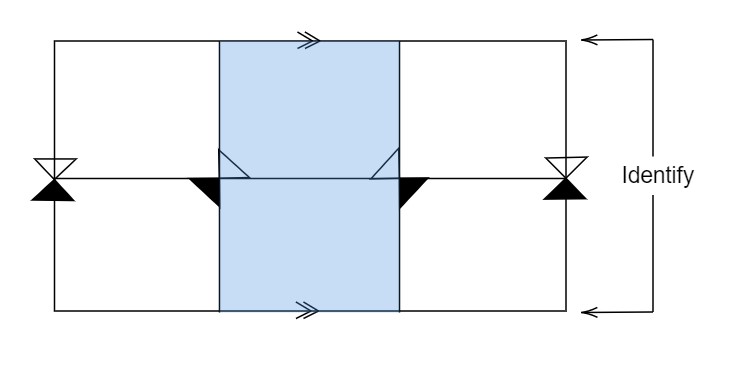
下図は、Non-totally viciousだがChronologicalではない時空の例である。
白と黒の三角形が光円錐で、白が未来向き、黒が過去向きを表している。
 画像の名前
画像の名前
Chronological時空は体積関数を用いて特徴付けることが出来る。
時空 $(M,g)$ がchronologicalであるための必要十分条件は、$t^\pm$ が任意の未来向きtimelike曲線に沿って狭義単調増加関数となることである。
$t^\pm$ が任意の未来向きtimelike曲線に沿って狭義単調増加関数であれば、chronologicalであることは自明である。
逆に、chronological時空であるとする。
もし $p<< q$ なる2点 $p,q\in M$ に対して、$t^-(p)=t^-(q)$ とする。
$I^-(q)\supset I^-(p)$ であるから、$I^-(q)\cap I^+(p)(\subset I^-(q))$ は測度0集合を除いて $I^-(p)$ に含まれる。
従って、$r\in I^-(q)\cap I^+(p)\cap I^-(p)$ が存在し、$p<< r<< p$ となる。
これはchronologicalであることに矛盾する。
$t^+$ に関しても同様である。
